Формула скорости

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

В чем измеряются?

Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать

Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема

Дальше будет сложнее. Давайте приступим:

S — расстояние — метр, километр , ;

v — скорость — метров в секунду, километров в час [м/с], [км/ч] (в случае может применяться километр в секунду;

t — время — секунда, минута, час , ,.

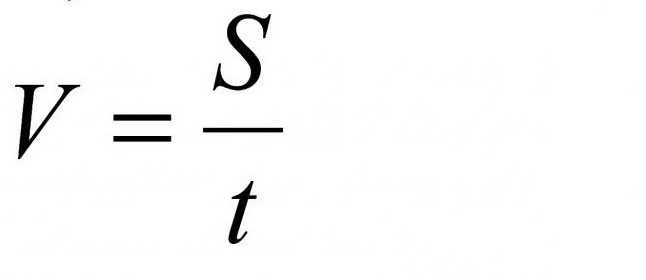
Обратите внимание, как обозначается скорость. Правильно, дробью

А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.

Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.

Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»

Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.

Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».

Итак, формула расстояния выглядит следующим образом: v×t=s

Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.

Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности. Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?

Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.

Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:

(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.

Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.

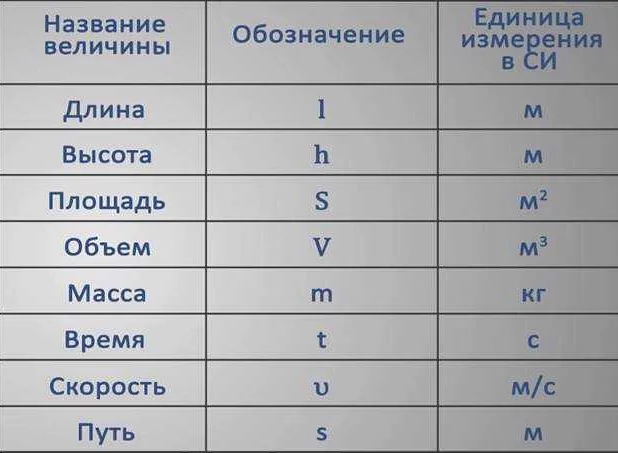
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Содержание урока

Примеры задач на нахождение скорости

Задача №1

Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.

Дано:$S = 152 \space км$$t = 3 \space ч$

$\upsilon -?$

Показать решение и ответ

Скрыть

Решение:

Скорость рассчитывается по формуле:$\upsilon = \frac{S}{t}$.

$\upsilon = \frac{152}{3} \frac{км}{ч} \approx 51 \frac{км}{ч}$.

Выразим в единицах СИ:$51 \frac{км}{ч} = \frac{51 000}{3600} \frac{м}{c} \approx 14 \frac{м}{c}$.

Ответ: $\upsilon = 14 \frac{м}{с}$.

Задача №2

Скорость лыжника первую часть пути составляла $20 \frac{км}{ч}$ в течение 15 мин. Следующие 45 мин его скорость была $10 \frac{км}{ч}$. Найдите среднюю скорость лыжника. 

Обозначим первую часть пути как $s_1$, вторую как $s_2$. Время, соответствующее движению на этих участках, $t_1$ и $t_2$ (рисунок 5). Скорости — $\upsilon_1$ и $\upsilon_2$.

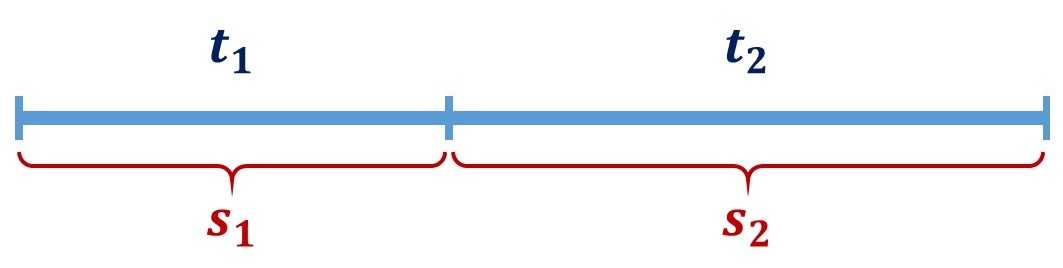
Рисунок 5. Схема движения лыжника

Дано:$\upsilon_1 = 20 \frac{км}{ч}$$t_1 = 15 \space мин$$\upsilon_2 = 10 \frac{км}{ч}$$t_2 = 45 \space мин$

$\upsilon_{ср} -?$

Показать решение и ответ

Скрыть

Решение:

Скорость лыжника на первой и второй частях пути:$\upsilon_1 = \frac{S_1}{t_1}$; $\upsilon_2 = \frac{S_2}{t_2}$.

Выразим из этих уравнений неизвестные $s_1$ и $s_2$:$s_1 = \upsilon_1t_1$; $s_2 = \upsilon_2t_2$.

Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:$\upsilon_{ср} = \frac{s_1+s_2}{t_1+t_2} = \frac{\upsilon_1t_1+\upsilon_2t_2}{ t_1+t_2}$.

Выпишем отдельно часть выражения и переведем в часы:$t_1+t_2 = 15 \space мин + 45 \space мин = 1\space ч$.Тогда:$t_1 = \frac{1}{4} \space ч = 0.25 \space ч$,$t_2 = \frac{3}{4} \space ч = 0.75 \space ч$.$\upsilon_{ср} = \frac{20 \frac{км}{ч} \cdot 0.25 \space ч+10 \frac{км}{ч} \cdot 0.75 \space ч}{1 \space ч} = \frac{5 \space км +7.5 \space км}{1 \space ч} = 12.5 \frac{км}{ч}$.

Ответ: $\upsilon_{ср} = 12,5 \frac{км}{ч}$.

Определение проводов

Рассматривая данный тип сети, можно выделить две вариации. Первая состоит из двух жил, вторая – из трех. Как можно понять, основное отличие между ними – в наличии или отсутствии проводника заземления (PE).

Двухпроводная проводка относится к устаревшему типу и встречается все реже. Такое проектирование разрешено ГОСТом и подходит для помещений с невысокими требованиями к безопасности. Используемая в старых домах двухжильная проводка TN-C имела совмещенную нейтраль и землю (PEN). С учетом современных требований, такая схема считается не безопасной.

Как и какими цветами маркируются жилы в двухпроводной однофазной проводке? Рассмотрим несколько вариантов:

Начиная с седьмой редакции ПУЭ (правила устройства электроустановок), электропроводка в квартире или доме должна осуществляться трехжильным кабелем с медными жилами (трехпроводная схема).

Рассмотрим, какие проводники входят в трехпроводную схему, и как они маркируются:

Ход урока

Организационный момент

Психологический настрой

Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.

Учитель
: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.

Сообщение темы и цели урока

Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.

(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).

Слайд № 1

Девиз нашего урока: «Один за всех, все за одного»

Работа в парах

На партах карточки с примерами:

Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)

Минутка чистописания

Слайд № 2

2 4 6 8 10 (образец в тетради)

Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?

Устная работа с остальными учениками:

В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?

Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?

Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?

За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?

Слайд № 3

Физминутка

Слайд № 4

Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор. (Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)

Первичное закрепление

Слайд № 5

Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?

Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?

Слайд № 6

Решение задачи № 2

Автобус

S — 90 км 90: 45= 2 часа
T — ?
V — 45 км/ч

Легковая машина

S — 270 км 270: 90 = 3 часа
T — ?
V — 90 км/ч

Давайте подведем итог урока

Чем занимались на уроке?

Что запомнили?

Рефлексия

Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.

• Красный — радость
• Жёлтый — приятное
• Зелёный — спокойное
• Синий — грустное
• Фиолетовый — тревожный
• Оранжевый — удовлетворение
• Чёрный — неудовлетворение

И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.

Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!

Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.

Измерительная система единиц

В физике существует много величин, для всех есть эталоны, и вся совокупность таких эталонов называется системой единиц. В системе единиц существуют базовые эталоны, которые определяются на основе явлений природы (например, метр изначально приравнивался одной сорокамиллионной части Парижского меридиана), и производные, определяемые на основе базовых (например, квадратный метр — эталон площади).

В настоящее время в мире действует единая система, которая называется СИ (фр. Système international d’unités, SI) и была принята Генеральной конференцией по мерам и весам (CGPM) в 1960 г. Единицы СИ представлены в следующей таблице:

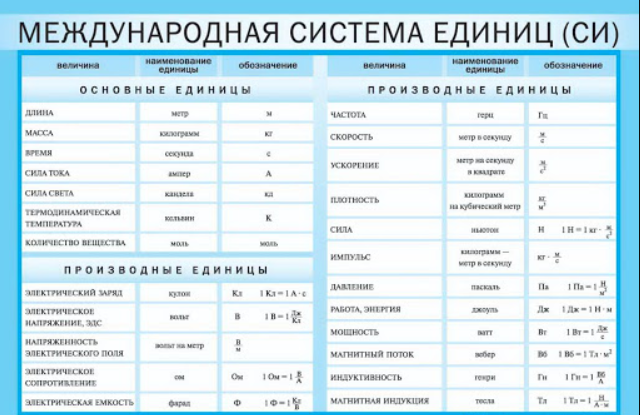Рис. 3. Таблица единиц.

Что мы узнали?

Физическая величина — это некоторое свойство рассматриваемого объекта или явления, которое можно измерить. Измерение физической величины означает сравнение ее с другой величиной такого же типа, принятой за эталон. Совокупность эталонов, принятая для измерений, называется системой единиц. В настоящее время действует система СИ.

1. /10

   Вопрос 1 из 10

История использования буквы «s» в математике

Буква «s» используется в математике для обозначения расстояния между двумя точками в пространстве. Однако вопрос о том, почему именно «s» была выбрана для этой цели, вызывает интерес не только у студентов математики, но и у исследователей этой науки.

История использования буквы «s» началась с греческой математики Евклида. В его трудах «Начала» буква «s» использовалась для обозначения длины линии. Позже, в средние века, буква «s» из единой линии превратилась в два сегмента, и тогда она стала использоваться для обозначения расстояний.

Также есть предположение, что буква «s» была выбрана для обозначения расстояния как сокращение слова «space» (пространство на английском языке). Это возможно, учитывая, что математика имеет многие термины на английском языке, традиционного для науки.

Несмотря на то, что история использования буквы «s» в математике не полностью ясна, её общеупотребительность и широкое распространение по всему миру говорят о том, что она является удобной и хорошо зарекомендовавшей себя обозначением.

Различные виды скорости

В физике скорость обозначается символом V. Он указывает на величину скорости и может быть использован для описания различных видов движения.

Существует несколько разновидностей скорости:

• Средняя скорость — это отношение пройденного расстояния к затраченному времени. Обычно обозначается символом Vср.
• Мгновенная скорость — это скорость в конкретный момент времени. Чтобы ее измерить, необходимо использовать инструмент для измерения малых промежутков времени.
• Относительная скорость — это скорость одного объекта относительно другого. Относительная скорость может быть как положительной, так и отрицательной, в зависимости от направления движения объектов.

Для более точного описания скорости в физике также используются другие понятия, такие как векторная скорость и скорость света.

Векторная скорость указывает не только на величину скорости, но и на направление движения. Обычно обозначается символом V с стрелкой над ним.

Скорость света (c) — это наивысшая известная скорость во вселенной. Символ «с» используется для обозначения конкретной скорости света в вакууме.

Название скорости	Символ
Средняя скорость	Vср
Мгновенная скорость	V
Относительная скорость	Vотн
Векторная скорость	V с стрелкой
Скорость света	c

В физике скорость является одним из основных понятий и широко используется для анализа и описания движения различных объектов.

Средняя скорость

Средняя скорость в физике обозначается символом v.

Средняя скорость — это отношение пройденного пути к времени, затраченному на его преодоление.

Формула для расчета средней скорости:

v = Δs / Δt

где Δs — пройденный путь (изменение координаты), а Δt — время, затраченное на преодоление данного пути.

Средняя скорость измеряется в единицах расстояния на единицу времени, например, метры в секунду (м/с).

Она является средним значением скорости на протяжении указанного интервала времени.

Средняя скорость может быть положительной (при движении вперед) или отрицательной (при движении назад).

Средняя скорость также может быть одинаковой для разных интервалов времени, но при этом траектория движения может быть разной. Например, при постоянной скорости аргумент Δs/Δt остается постоянным.

Мгновенная скорость

Мгновенная скорость — это скорость тела в определенный момент времени или в конкретной точке. Она показывает, как быстро объект движется в данное время или на данном участке пути.

Для обозначения мгновенной скорости в физике используется символ v.

Для определения мгновенной скорости необходимо знать путь, пройденный объектом в определенный момент времени, и время, за которое объект преодолел этот путь. Результат измерения мгновенной скорости выражается в единицах длины, например в метрах в секунду (м/с) или километрах в час (км/ч).

Мгновенная скорость может быть как положительной, так и отрицательной, в зависимости от направления движения объекта. Положительное значение скорости указывает на движение вперед, а отрицательное — на движение назад. Скорость равна нулю, если объект не движется.

Для более точной оценки мгновенной скорости, иногда прибегают к использованию математических методов, таких как дифференциальное исчисление. Это позволяет определить изменение скорости при бесконечно малом временном интервале.

Относительная скорость

В физике символ в обозначает скорость. Однако, когда речь идет о скорости объекта относительно другого объекта, используется понятие относительной скорости.

Относительная скорость — это разница между скоростями двух объектов, движущихся относительно друг друга. Она показывает, насколько быстро объекты приближаются друг к другу или отдаляются друг от друга.

Для вычисления относительной скорости необходимо знать скорости каждого объекта и направления их движения. При этом скорость одного объекта выбирается в качестве опорной, и скорость второго объекта относительно первого рассчитывается.

Относительная скорость может быть положительной, если объекты приближаются друг к другу, и отрицательной, если объекты отдаляются друг от друга.

Вычисление относительной скорости может быть полезно в различных областях физики, например, в механике, астрономии, аэродинамике и других.

Скорость при равномерном движении

Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?

Рисунок 1. Разные физические тела, совершающие равномерное движение

В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь в физике появляется такая величина, как скорость.

В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, то есть движутся с различными скоростями.

Что показывает скорость при равномерном движении?

{"questions":,"answer":}}}]}

Как применять скорость в решении задач

Скорость – это физическая величина, обозначающая изменение расстояния за единицу времени. В математике скорость часто используется при решении задач на движение.

Для применения скорости в решении задач необходимо:

1. Определить начальное и конечное расстояния
2. Найти разницу между начальным и конечным расстоянием, чтобы определить пройденное расстояние
3. Определить время, за которое было пройдено расстояние, чтобы найти скорость

Следует обратить внимание на единицы измерения скорости. В Международной системе единиц скорость измеряется в м/с, а народной – в км/ч

При решении задач необходимо использовать одну из единиц измерения.

Знание скорости позволяет не только решать задачи на движение, но и оценивать время, необходимое на перемещение в определенном направлении. Скорость также помогает оценить возможности объекта и понимать, как изменится перемещение объекта при изменении скорости.

В заключение, для того чтобы успешно решать задачи на движение, нужно знать как работает скорость и уметь применять ее в решении задач. Понимание принципов скорости поможет улучшить практические навыки решения задач на движение и применять их в повседневной жизни.

В чем измеряются?

Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать

Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема

Дальше будет сложнее. Давайте приступим:

S — расстояние — метр, километр , ;

v — скорость — метров в секунду, километров в час [м/с], [км/ч] (в случае может применяться километр в секунду;

t — время — секунда, минута, час , ,.

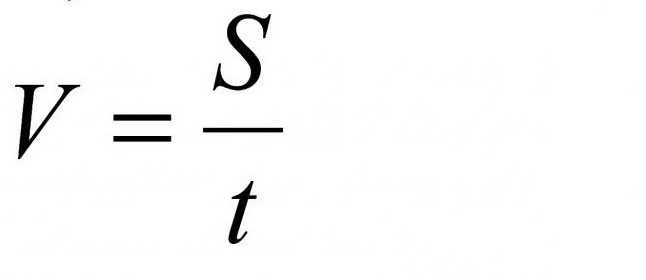
Обратите внимание, как обозначается скорость. Правильно, дробью

А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.

Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.

Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»

Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.

Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».

Итак, формула расстояния выглядит следующим образом: v×t=s

Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.

Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности. Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?

Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.

Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:

(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.

Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.

Примеры решения задач

Задание. Движение материальной точки А задано уравнением: $x=2 t^-4 t^$ . Точка начала свое движение при t=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$ \begin10 t-t^=10(2.2) \\ t_=5+\sqrt \approx 8,8(c) ; t_=5-\sqrt \approx 1,13(c) \end $$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

При решении уравнения (2.3) нам подойдет корень равный:

Ответ. 1) $x=0 \mathrm

m>$ 2) $t_=8,8 \mathrm, t_=1,13 c, t_=11 c$

Расстояние

Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).

Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.

Расстояние связано со скоростью и временем:

S=v \cdot t

Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.

Единицы длины	СИ
1 сантиметр	0,01 м
1 километр	1000 м
1 дециметр	0,1 м
1 миллиметр	0,001 м
1 микрометр	1·10-6 м
1 миля	1609,34 м
1 фут	0,3048 м
1 ярд	0,9144 м
1 дюйм	0,0254 м
1 морская миля	1852 м