Решить за 60 секунд. как 51-летний учитель рвет tik-tok уроками математики

Содержание

Слайд 1
Слайд 2

Голландский физик, математик и химик Фриц Цернике в 1930 году начал работать в области оптики. В этом же году он открыл фазово-контрастный метод. В течение 1930—1940-х годов Цернике внёс свой вклад и в других вопросах оптики, в то время как фазово-контрастный метод не был замечен широкими кругами учёных. Новый метод оставался вне поля зрения научного сообщества вплоть до Второй мировой войны, когда во время немецкой оккупации Голландии открытие Цернике было использовано для создания первых фазово-контрастных микроскопов.
В течение войны многие производители стали выпускать фазово-контрастные микроскопы, и они стали широко применяться в биологических и медицинских исследованиях.
Слайд 3

Фазово-контрастная микроскопия является видом оптической микроскопии, которая преобразует фазовые сдвиги в свет, проходящий через прозрачный образец для изменения яркости в изображении. Фазовые сдвиги сами невидимы, но становятся видимыми, как изменения яркости.
Фазово-контрастная микроскопия особенно важна в биологии, так как он раскрывает многие клеточные структуры, которые не видны с простыми световых микроскопов . Эти структуры были видны ранее биологам при окрашивании препаратов. Это требовало дополнительной подготовки, в результате которой погибали клетки. Фазово-контрастная микроскопия позволила биологам изучать живых клеток и видеть как они размножаются путем деления.
Слайд 4

Когда световые волны проходит через среду отличную от вакуума, взаимодействие со средой приводит к тому, что волны изменяют амплитуду и фазу, по характеру, зависящему от свойств среды. Изменения амплитуды (яркости) возникают в результате рассеяния и поглощения света, которые, зачастую, зависят от длины волны и может привести к возникновению цветов. Фототехника и человеческого глаза чувствительны только к вариации амплитуды. Без специальной договоренности, фазовые изменения невидимы. Тем не менее, часто эти изменения фаз несут важную информацию.
Фазово-контрастной микроскопии сделала такой прогресс в микроскопии, что его изобретатель Фриц Цернике был удостоен Нобелевской премии (физика) в 1953 году.
Слайд 5

Для получения фазовоконтрастного изображения свет от источника разбивается на два когерентных световых луча, один из них называют опорным, другой предметным, которые проходят разные оптические пути. Микроскоп юстируют таким образом, чтобы в фокальной плоскости, где формируется изображение, интерференция между этими двумя лучами гасила бы их.
Длину оптического пути изменяют с помощью, так называемой, фазовой пластинки, расположенной на фазовом кольце. Когда на пути одного из лучей находится образец, преломление света в нём изменяет оптический путь, а, следовательно, и фазу, что изменяет условия интерференции.
Слайд 6
Слайд 7
Слайд 8

Посмотреть все слайды

Дмитрий Щигарев, победитель, БОУ ВО «Вологодский многопрофильный лицей», 11 класс, Череповец

Как вышел на всеросс?

Мне всегда нравилась физика. Как сказал один мой знакомый, выбирая между физикой, химией и математикой: «В математике надо быть очень умным, в химии — очень много знать, а в физике — и то, и другое, но немножко».

До девятого класса я учился в обычной школе, любил физику, математику, ходил на множество кружков по авиамоделированию, электроконструированию… Далее осознал, что мне наскучила простая школьная жизнь. Однажды меня позвали в специализированный лицей, куда я и перешел. Первые полгода я страдал: 11 часов школа и еще четыре — домашка. Было тяжело, но я подружился с нашим преподавателем по физике и уже начал готовиться к олимпиадам. В среднем олимпиадная подготовка тогда занимала по 3-4 часа в день. Вскоре я затащил регион, съездил в «Сириус». На заключительном этапе до диплома мне не хватило совсем немного. Было немного жаль, но я понимал, что за полгода подготовки достиг отличного результата: 70-е место на всероссе — это очень неплохо. Далее я готовился уже меньше, около двух часов день, но главное — регулярно. В 10-м классе я прошел на всеросс, который отменили. На отборе я стал примерно 40-м и не вышел на межнар. Примерно сохраняя график подготовки, я прошел на всеросс и в 11-м классе.

Какие ощущения от олимпиады в этом году?

Задания были хорошие, заставили поразмышлять. Мне повезло на этом всероссе, и я смог получить диплом победителя. Хотя я знаю ребят, которые разбираются в предмете лучше меня, готовились больше, но не смогли разглядеть идеи задач и получили дипломы призеров. Фактически олимпиада — это 50% везения и 50% «нарешенности» с талантом.

Из-за ковида всеросс выдался коротким. Туры шли подряд, без обычного однодневного перерыва между ними, поэтому отсутствовало время на культурную программу. Была проведена заочная апелляция с длинными очередями и небольшой сложностью в общении (не у всех стабильный интернет, есть посторонние шумы и т. п.). Да и времени пообщаться с друзьями было не так и много.

Отличается ли уровень подготовки ребят из Москвы и регионов?

Уровень подготовки ребят оказался крайне неодинаковым. У меня есть множество примеров, когда человек из, например, Краснодарского края или даже Нижнего Новгорода переезжает в столичный город. Причин тому много: высокая концентрация «звёздных» преподавателей, большие премии за результаты на всероссе, отсутствие технической базы и хороших преподавателей на малой родине (хотя недавно начали строить центры типа «Сириуса» в регионах, но до их нормальной работы ещё далеко). Также зачастую талантливого человека из нестоличного региона тянет назад общество друзей, не вовлеченных в олимпиадное движение (я учусь в лицее, где множество олимпиадников, и поначалу я втягивался в это общество). Хотя есть некоторые регионы и города, где находятся мощные школы, например, Татарстан, Саранск, Коми, Вологда, Томск. Но они всё равно отстают как по уровню подготовки, так и по количеству участников.

1970-е

год	человек	страна	Причина присуждения премии
1970 г.	Ханнес Альфвен (1908-1995)	Швеция	«За фундаментальные достижения и открытия в магнитогидродинамике с плодотворными применениями в различных областях физики плазмы »
Луи Неэль (1904-2000)	Франция	«За фундаментальные достижения и открытия в области антиферромагнетизма и ферримагнетизма , которые привели к важным приложениям в »
1971 г.	Деннис Габор (1900–1979)	Соединенное Королевство (родился в Будапеште , Венгрия )	«За изобретение и развитие голографического метода »
1972 г.	Джон Бардин (1908-1991)	США	«За совместно разработанную теорию сверхпроводимости , также известную как теория БКШ »
Леон Нил Купер (1930 г.р.)	США
Джон Роберт Шриффер (1931-2019)	США
1973	Лео Эсаки (* 1925)	Япония	«За экспериментальные открытия, касающиеся туннельного явления в полупроводниках или сверхпроводниках»
Ивар Гиавер (родился в 1929 г.)	США (родился в Бергене , Норвегия )
Брайан Дэвид Джозефсон (1940 г.р.)	Объединенное Королевство	«За теоретическое предсказание свойств сверхтока через туннельный барьер, особенно тех явлений, которые обычно известны как эффект Джозефсона »
1974 г.	Мартин Райл (1918-1984)	Объединенное Королевство	«За новаторскую работу в радиоастрономии : Райл за его наблюдения и изобретения, особенно в технологии синтеза апертуры, и Хьюиш за его решающую роль в открытии пульсаров »
Энтони Хьюиш (* 1924)	Объединенное Королевство
1975 г.	Оге Нильс Бор (1922-2009)	Дания	«За открытие связи между коллективным движением и движением частиц в атомных ядрах и развитие теории строения атомных ядер, основанной на этой связи»
Бен Моттельсон (* 1926)	Дания (родился в Чикаго , Иллинойс , США )
Джеймс Рейнуотер (1917-1986)	США
1976 г.	Бертон Рихтер (1931-2018)	США	«За ведущие достижения в открытии тяжелой элементарной частицы нового типа »
Самуэль Чао Чунг Тинг (* 1936)	США
1977 г.	Филип Уоррен Андерсон (1923-2020)	США	«За основные теоретические достижения по электронной структуре в магнитных и неупорядоченных системах»
Невилл Фрэнсис Мотт (1905-1996)	Объединенное Королевство
Джон Хасбрук Ван Флек (1899-1980)	США
1978 г.	Петр Капиза (1894-1984)	Советский Союз	«За фундаментальные изобретения и открытия в области физики низких температур »
Арно Пензиас (* 1933)	США (родился в Мюнхене , Германия )	«За открытие космического микроволнового фонового излучения »
Роберт Вудро Вильсон (* 1936)	США
1979 г.	Стекло Шелдона Ли (* 1932)	США	«За вклад в теорию единого слабого и электромагнитного взаимодействия элементарных частиц, в том числе в том числе. предсказание слабых нейтральных токов »( электрослабое взаимодействие )
Абдус Салам (1926–1996)	Пакистан (родился в Джанг , Британская Индия )
Стивен Вайнберг (1933-2021)	США

Андрей Минаков, победитель, КГБОУ «Бийский лицей-интернат Алтайского края», 10 класс, Бийск

Как вышел на всеросс?

В течение 2,5 лет я регулярно занимался олимпиадной физикой (у меня было 4 пары в неделю) и иногда, 1-2 раза в год, ездил на сборы. За месяц до регионального этапа количество пар увеличилось до 7 в неделю, а затем подготовка стала ещё интенсивнее: 1-2 пары в день и решение на скорость олимпиад, которые нам давал преподаватель. Мы часто решали номера из задачника «Кванта» со всероссов прошлых лет — как экспериментальные, так и теоретические. Пару раз нам давали даже задачи со сборов по подготовке к межнару. Благодаря всему этому я и попал на всеросс.

Какие ощущения от олимпиады в этом году?

Я ощущал волнение, так как впервые выступал на заключительном этапе. Думал, что напишу гораздо хуже, поэтому своим результатом я более чем доволен.

Организация олимпиады могла бы быть и лучше. Например, запись инструктажа перед экспериментальным туром выложили тогда, когда мы в автобусе ехали из гостиницы на этот самый экспериментальный тур. Да и коронавирус всё испортил: всё прошло очень быстро, не удалось даже пообщаться со старыми знакомыми, которых давно не видел.

Какие планы на будущее?

В ближайшем будущем собираюсь ботать, ботать и ещё раз ботать. Никаких определенных планов у меня нет. Сейчас идет подготовка к Балтийской олимпиаде, на которую меня пригласили. Насчет вуза еще не задумывался. Разумеется, что-то связанное с физикой.

Прыгнул на спинку стула, как Валерий Сюткин в клипе

— В классе вы прошли тему, сделали контрольную работу. Поняли, кто как усвоил

Вам важно, чтобы материал в сети тоже усваивался? Как это понять?

— Конечно, важно, чтобы усваивался. Иначе зачем тогда все делаем? Как проверить знания в сети? Никак

Могу судить о чем-то только по комментариям. Иногда благодарят — мол, тему понял за 40 секунд, хотя прежде не мог разобраться в течение трех уроков.

Уверен, что из пяти миллионов человек кто-то все равно вникает в тему. Иначе зачем нужно подписываться на наши уведомления о появлении новых роликов? Значит, это полезно.

— Обратная связь есть? Вам пишут?

— Конечно. И «ВКонтакте» пишут, и на электронную почту. И дети, и взрослые. В YouTube я решил пресловутую задачу по геометрии под номером 337. Она набрала очень много просмотров. Но мое решение было замысловатым, и вот я получаю письмо со сказочным вариантом решения этой задачи.

Я записал ролик с этим решением и упоминанием автора — Владимира Гаркуши, нашего подписчика, увлеченного геометрией. Его вариант решения показал в Москве математику Алексею Владимировичу Савватееву. Он был в восторге.

— В одном из своих роликов на YouTube вы запрыгиваете на стул и лихо спрыгиваете с его спинки, удерживая равновесие. Когда стали блогером, пришлось обучиться каким-то штукам специально, чтобы удивить аудиторию?

— Это я умел. Мне было лет двадцать, когда увидел в клипе группы «Браво», как подобный несложный трюк делает Валерий Сюткин, когда про оранжевый галстук поет. Я подумал — как интересно, а у меня получится? Чисто математически рассчитал, оказалось несложно и совсем безопасно.

Когда мы записывали тот ролик, я решил сделать что-то не особо интеллектуальное, а после перейти к интеллекту.

Элемент шоу присутствует в наших роликах, но не всегда. А вот самоиронию использую часто.

— С темой буллинга в сети сталкивались, как вы отвечаете троллям?

— Я его не ощущаю. Во-первых, мне за пятьдесят, я состоявшийся мужчина. И вдруг какой-то комментарий выведет из себя? Нет. Но если укажут на ошибку — такое случается — критику по существу приму.

Не терплю всякого рода ксенофобию, если вижу оскорбительные комментарии или нецензурную брань — сразу удаляю. Слежу за доброжелательностью обстановки.

— Вот вы — учитель, а своим детям приходилось математику объяснять? Проще это или сложнее?

— Может быть, даже сложнее. Иногда сдержаться бы, если вдруг понимаешь, что правило, которое должно быть выучено, твой ребенок не знает. Сейчас двое сдают ЕГЭ. У нас вообще свободно с этим. Не понял что-то — подойди, спроси. Если долгое время не подходят, спрашиваю сам, все ли понятно по пройденным темам.

Петр Земсков вместе с младшим сыном Андреем. Малыш любит полистать учебник геометрии

Основные труды

В 1930 году Цернике, проводя исследования по спектральным линиям, обнаружил, что так называемые спектральные духи, которые находятся слева и справа от каждой основной линии в спектрах, созданных с помощью дифракционной решётки, имеют сдвиг по фазе от первичной линии на 90 градусов. В 1933 году на физическом и медицинском конгрессе в г. Вагенинген Цернике впервые описал свой метод фазового контраста в приложении к микроскопии. Он использовал метод, чтобы проверить форму вогнутых зеркал. Его открытие легло в основу первого микроскопа на основе метода фазового контраста, построенного во время Второй мировой войны.

Ещё один вклад в области оптики связан с эффективным описанием дефектов изображений или аберраций оптических систем, таких как микроскопы и телескопы. Представление аберраций первоначально было основано на теории, разработанной Людвигом Зейделем в середине девятнадцатого века. Представление Зейделя было основано на разложении в степенной ряд и не позволяло провести чёткое разделение между различными типами и порядками аберраций. Ортогональные многочлены Цернике позволили решить эту давнюю проблему оптимальной «балансировки» различных аберраций оптических систем. С 1960-х полиномы Цернике широко используются в оптическом дизайне, оптической метрологии и анализе изображений.

Работы Цернике помогли пробудить интерес к теории когерентности, исследованиям частично когерентных источников света. В 1938 году он опубликовал более простой вывод теоремы ван Циттерта (1934 год) о когерентности излучения от удалённых источников, ныне известной как теорема ван Циттерта — Цернике.

Скажет: «Я — гуманитарий», — и учить не будет

— Петр Александрович, принято делить людей, особенно в школе, на гуманитариев и технарей. И если ребенок схватил «трояк», родители махнут рукой: «Ну, ты у меня гуманитарий». Действительно ли, если ребенок не математик, надо отстать от него? Правильно ли так успокаивать?

— Разделение на гуманитариев и технарей часто звучит как оправдание. Человек себе придумал отговорку «я — гуманитарий» вместо того, чтобы потрудиться, выучить правило по геометрии и попробовать его применить.

Я считаю, что школьную программу способен осилить любой человек, хотя бы базовые вещи. Необязательно решать задачи со звездочкой.

Если мы будем поощрять ребенка в том, что он — гуманитарий, или сами оправдывать результат его неуспешной учебы, порой просто прикроем лень.

Умственный труд — тоже труд.

Смотрите, что происходит после начальной школы. Там все понятно и просто — два яблока, пять яблок. Писать умеют все, читать умеют все, считать мало-мальски — тоже. И все думают, что учеба — это легкотня.

На самом деле это умственное преодоление. Такое же, как физическое, когда, например, нужно покорить вершину горы. Чтобы подняться туда, надо напрячь волю, заставить себя и пойти. И вот есть задача, которую ты не понял. Но есть голова, воля и учитель, который может помочь.

— Вам встречались такие, кто все-таки не понимал? И что вы тогда делали?

— Я все же считаю, что такое бывает, если ученик запустил учебу, перестал выполнять домашние задания.

Был у меня один случай. Объяснил уже не раз ученику задачу, но он не может ее решить, и тогда я, человек не особенно воцерковленный, начал читать «Отче наш» (Петр Александрович читает молитву вслух). И вы представляете — он тут же ее и решил! Потом разговаривал со знакомым священником, рассказал ему эту историю — вон чего сила молитвы творит.

Я стараюсь, чтобы дети поняли тему. Мне можно задать вопрос на любой стадии урока или на перемене. Если кто-то не понял, вижу в классе того, кто понял, предлагаю ему поделиться опытом с одноклассником.

Но тут некоторые говорят, что тем самым я как бы акцентирую внимание на том, кто понял, а кто — нет. Но урок же не соревнование, кто лучше понял

Вот я пятиклассников веду, выполняем самостоятельную, и вдруг бежит один — «я сделал!» Другой бежит, и я вижу, что начальная школа — некий соревновательный процесс.

Но мы-то просто учимся решать задачи, которые нам помогают решать другие задачи, жизненные.

— Но существуют же склонности к тем или иным наукам, как вы думаете?

«Вычисляю квадратный корень, покрываясь холодным потом». Почему мы боимся математики

— Наверное, да. Кто-то легко справляется, без напряга. Другой — наоборот. Ну, вот пример. Два ученика, оба сдают экзамен. Один ничего не учил, один раз прочитал, что квадрат гипотенузы равен сумме квадратов катетов, и как-то все легко понял и запомнил. Доказательство теоремы было на уроке. Он пришел на экзамен и быстренько все доказал, применил.

Второй ребенок. Теорема Пифагора — квадрат чего? А-а-а, гипотенузы. Надо выучить. Он три часа учил формулировку, четыре — доказательство теоремы, к утру натренировался применять это в задачах. Пришел и также все ответил.

Один большим трудом достиг результата, а другой — на одном таланте, памяти. Оба получили «пять».

— Тут ситуация такая, когда учитель может и задуматься, какую оценку ставить?

— По факту — оба сделали. Я за то, чтобы обоим — пятерки. Но иногда возникают ситуации, когда учитель думает: этот талантливый, потому ему — «пять», а другому — «четыре». Или наоборот: этот — трудился, он молодец, ему «пять», а другому — «четыре», потому что если бы занимался, мог бы еще лучше.

Такого разделения быть не должно. Ну вот техника чтения, к примеру. Весь класс читает 200 слов в минуту, а один ученик — 180 слов. Норматив — 150. У всех должны быть пятерки.

Мы ставим оценки не в сравнении знаний и умений учеников, а по нормативу.

Константин Циолковский

Будущий основатель современной космонавтики с детства страдал от тугоухости. Она стала последствием скарлатины, перенесенной ученым в возрасте 10 лет. Мальчику было сложно воспринимать обрывки фраз учителя, и без слуховых аппаратов он был обречен на плохую учебу. В Вятской мужской гимназии Циолковский слыл хулиганом и часто попадал в карцер. Во втором классе остался на второй год, а из третьего вообще был исключен за неуспеваемость. Впрочем, дело, видимо, было не в отсутствии способностей, а в нехватке мотивации, так как спустя 6 лет Циолковский успешно сдал экзамены на звание учителя и получил официальное направление от Министерства просвещения.

Тот мальчик в капюшоне — самый лучший для своей мамы

— Какие они — современные дети? Что их отличает от других поколений?

— Когда мои друзья интересуются, предполагают, что дети сейчас — ужас какие, я всегда говорю, что они однозначно лучше нас. Да, совершают иногда нелицеприятные поступки, но не от того, что хотя насолить учителю.

От недостатка воспитания ученик может что-то выкрикнуть. И тогда ты спрашиваешь: «Женя, Саша, что это было? Тебе 15 лет. Аркадий Гайдар в твоем возрасте дивизией командовал». Им уже интересно — кто такой Гайдар? Рассказываю.

Тут дело вот в чем. Разница поколений. Вот мне 51 год, я совсем из другого поколения. Я и мой отец еще понимаем друг друга, у нас одинаковый уровень цитирования. Мы с ним в каких-то базовых моментах одинаковые.

Он для меня авторитет только потому, что старше и опытнее. И если он мне говорит — держи пилу определенным образом и пили определенным образом, я ему поверю просто так. Мне не нужно это с ним обсуждать, я просто выполняю

А теперь внимание!

Когда я объясняю поколению Z — младшим школьникам — условно про то, как пилить, мне задают вопрос: «А почему именно так? Почему правой рукой? Почему прижимать нужно именно коленом?»

Хочется сказать: «Слушай, мне 50 лет, я сто раз отпиливал бруски — я знаю, как удобнее». Но сейчас это не работает. Ты либо помогать его не зови, либо объясняй все подробно, аргументируй, убеждай.

— Что вас особенно трогает из того, что слышите от детей?

— Дети иногда говорят: «А почему это сделать должен именно я? Ведь я такой же, как все…» Мгновенно вспыхиваю и говорю: «Когда отцу твоему выдали тебя в роддоме, он взял тебя на руки, и вместе с матерью они потихонечку пошли к машине, привезли маленький кулечек домой, с тех пор вся их жизнь крутилась вокруг тебя. Потому что ты — самый лучший на Земле. По крайней мере для вот этих двух человек. Тебя родили, чтобы ты стал лучшим. А ты как все собираешься жить. Мать купила тебе лучшие штаны, такой кепки не было ни у кого во всем дворе, отец тебе купил самый лучший велосипед! И у каждого из вас — так! Вот вы можете представить, что сейчас мне урок срывает лучший человек на Земле?»

Я все время помню о том, что тот самый мальчишка в классе, который сидит на задней парте и ему все время говорят: «Сними капюшон на уроке» — самый лучший для своей матери.

— Какие три качества вы считаете самыми важными для современного учителя?

— Расскажу историю, которая и будет ответом на вопрос. Однажды, когда мы учились в институте, наши девчонки делали стенгазету. Взяли интервью у преподавателя и спросили примерно об этом же. Он ответил, что прежде всего — высокая духовность.

И это все? А как же любовь к детям, к предмету? Но все это и складывается из твоего внутреннего состояния. Будучи высокодуховным человеком, ты же не пойдешь учить детей, если не можешь с ними ладить? Ты же не пойдешь преподавать математику, если не знаешь ее?

Достоинство ученика и учителя. Это базовые вещи. Они неприкасаемы. Ученик — такой же человек, он чувствует так же, как ты. К нему нужно относиться с уважением.

На моих уроках нет повелительного тона — «Встали! Сели!» Я говорю: «Прошу встать», «Прошу сесть». Но если кто-то шумит, могу замолчать. Не потому что я такой крутой, а потому что учитель не имеет права давать урок, когда кто-то его не слышит. Иначе это означает, что ученик не усвоит тему.

Работаю в лицее, и если что-то не так с поведением, всегда напоминаю ученикам о лицеистах другого века — Пушкине, например. Всегда есть на кого равняться.

Поскольку вы здесь…

У нас есть небольшая просьба. Эту историю удалось рассказать благодаря поддержке читателей. Даже самое небольшое ежемесячное пожертвование помогает работать редакции и создавать важные материалы для людей.

Сейчас ваша помощь нужна как никогда.

ПОМОЧЬ

Цыфиркин

Цыфиркин учит Митрофанушку арифметике. Он является отставным сержантом, который после двадцатилетней службы подрабатывает тем, что пытается помогать безграмотным чиновникам со счетом потому, что сами они считать не усеют. В свободное время он учит детей. Но Митрофанушку он не может ничему научить по нескольким причинам. Во-первых, он сам знает не так много, чтобы учить. Во-вторых, его ученик – лентяй и бездельник. Он глуп и не способен к обучению. В итоге после двух лет обучения Митрофанушка не научился считать. Но для Цыфиркина оказывается важна честь и правда. Он отказывается от вознаграждения, так как результат не получен. Именно за это Стродум и Милон награждают учителя.

Индивидуальные доказательства

Страна по информации на nobelprize.org. Страна может отличаться от национальности лауреата.
под этим именем в официальные списки Нобелевского фонда. Сегодня более распространено название Братислава .
↑ Деньги переданы в специальный фонд этой ценовой категории.
↑ Одна треть призовых была передана в основной фонд, а две трети — в специальный фонд этой призовой категории.
↑ Страна происхождения лауреатов премии 1957 года отмечена в официальных списках как «Китай». В то время, когда лауреаты премии эмигрировали, Китаем все еще правила Китайская Республика . На момент вручения награды Китайская Республика все еще была официальным международным представителем Китая на Тайване .
Обычно места рождения указываются в официальных списках Нобелевского фонда, если они не находятся в указанном государстве или не находились в то время под суверенитетом этого государства. Однако здесь эта информация отсутствует.

Контекст

Константин Эдуардович Циолковский (1857–1935), идейный вдохновитель воздухоплавания и космонавтики, занимался научными и фантастическими идеями в свободное время, а на жизнь зарабатывал учительским трудом. Систематического образования он не получил, так как в детстве оглох из-за скарлатины, но проучился четыре года в Вятской гимназии, а потом занимался самообразованием, в том числе три года — в Москве, в библиотеке по книгам. В 1876 году вернулся в Вятку, где жил его отец, и занялся репетиторством. Затем семья переехала в Рязань, и именно там Константин в 1879 году экстерном сдал экзамен на звание народного учителя. Кстати, произошло это в его день рождения — ему исполнилось 22 года.

Спустя четыре месяца он получил назначение учителем арифметики и геометрии в Боровское городское училище. До 1921 года преподавал математику и физику в учебных заведениях Боровска и Калуги, в том числе в дореволюционный период — в женском епархиальном училище, а с 1918 года — в трудовой школе. В 1906 году был награждён за учительские успехи орденом Св. Станислава третьей степени. Работу в школе прекратил в 1921 году по состоянию здоровья.

Хотя, вспоминая свои первые шаги на учительском поприще, Циолковский и написал, что «педагогия» была для него забавой, в дальнейшем учительство его увлекло. Преподавателем он был по тогдашним меркам необычным: старался не давить на детей и делать уроки интересными для них, считал непедагогичным ставить плохие отметки. Глухота, конечно, осложняла ему работу, но не делала её совсем невозможной. Слушая ответы учеников, он прикладывал руку к уху, а позднее устроил себе особую слуховую трубу.

В 1932 году, когда Константину Эдуардовичу было уже 75 лет, он подвёл такой итог своей жизни: «Может быть, мои изобретения не осуществятся. Вот то, что я работал 40 лет учителем, я считаю несомненной заслугой».

Экзамен, о котором идёт речь в его воспоминаниях, был введён распоряжением Министерства народного просвещения в 1874 году. Получить звание учителя городского училища в то время можно было и без аттестатов, дипломов или свидетельств об окончании педагогических курсов — но требовалось сдать экзамен специальной комиссии. Испытания проводили по Закону Божию, русскому языку и словесности, математике, истории, географии, естествознанию, физике, а также по «искусствам» — черчению, рисованию, чистописанию.

Сверх испытаний, надо было провести пробные уроки — по русскому языку, арифметике алгебре или геометрии и естествознанию (естественной истории, как тогда называли этот предмет).

От «теории капризов» к атомной бомбе

Так один эксперимент привел к появлению целой теории, которую Семенов сравнивал с капризами природы: «В физике, как известно, «капризов» практически нет, в то же время биология полна ими. Химия занимает промежуточное положение: иногда реакция течет нормально, а иногда — сплошные «капризы». Цепная теория — это «теория капризов» химического превращения…»

И это был лишь один опыт в «лаборатории странных явлений» Семенова. А их было множество: по теории теплового взрыва, тепловой теории пробоя диэлектриков, теории молекулярных пучков, по первому применению масс-спектроскопии в химии и др. Если в 1920 году Семенов был в своей лаборатории один, то к 1930-му у него в подчинении было уже 50 молодых ученых, которых он выбрал и подготовил сам. «В те годы рост знаний и опыта у представителей талантливой молодежи был поразителен. Все они к этому возрасту (25 лет) имели уже по несколько печатных работ, порою обладавших существенно пионерским значением в масштабе всей мировой науки. На эти работы широко ссылались в своих трудах иностранные ученые», — вспоминал Семенов о своей лаборатории, которая в 1931 году превратилась в Институт химической физики Академии наук СССР под его руководством.

В должности академика, профессора, директора Семенов продолжал работать в области химической физики как ученый. Результаты его исследований процессов взрыва, горения и детонации в 1940-е годы использовались в производстве патронов, артиллерийских снарядов, взрывчатых веществ, зажигательных смесей, при создании гранат и мин в борьбе с вражескими танками. Так что Семенов внес свою лепту в нашу победу в Великой Отечественной войне.

В 1940-е и 1950-е годы он занимался советской атомной программой и участвовал в ядерных испытаниях, но, поняв их военный потенциал, позже принимал активное участие в движении ученых против угрозы ядерной войны, присоединившись к Пагуошскому движению. За 90 лет жизни Семенов успел очень многое, в том числе сумел создать семеновскую школу на стыке наук — физики, химии и биологии. За свою научную деятельность он был удостоен Ленинской премии, дважды — Государственной премий СССР, дважды – звания Героя Социалистического Труда, награжден девятью орденами Ленина, орденом Трудового Красного Знамени и удостоен высшей награды Академии наук — золотой медали им. М. В. Ломоносова. 14 иностранных академий наук избрали Семенова в свой состав и восемь известных университетов мира присудили ему почетную степень honoris causa. В конце жизни Николай Николаевич сохранял активность, был вице-президентом Академии наук, в 75 лет женился на молодой аспирантке третьим браком, с 1981 года работал главным редактором журнала «Химическая физика».

Один из внуков вспоминал, что дед Коля работал даже в выходные, но все же находил время собраться вместе с семьей за большим столом. «Дед любил компанию и веселое застолье, — писал внук ученого А. Ю. Семенов. — Часто на выходные или на праздники собирались многочисленные друзья, родственники и ученики — сотрудники созданного им Института химической физики. Не обладая хорошим слухом, дед тем не менее любил петь. Мне запомнилось, как он поет песню «Эх, Самара-городок». Дед часто смеялся — негромко, но очень заразительно. Еще чаще он щурился и улыбался в усы».

8.1. Разложение волновой аберрации в ряд по полиномам Цернике

При вычислении разнообразных характеристик качества изображения требуется вычисление через в большом количестве точек на зрачке, до нескольких сотен. Для того чтобы заменить весьма трудоемкий расчет большого числа лучей простыми алгебраическими действиями, необходима численная
модель . Поэтому функция волновых аберраций представляется в виде ряда по степеням зрачковых координат или по другим функциям этих координат.
Разложение по степенным координатам подробно рассматривается в параграфе .

8.1.1. Разложение волновой аберрации по полиномам Цернике

Альтернативой степенному базису служат полиномы, введенные в оптику голландским ученым, лауреатом Нобелевской премии по оптике, Фрицем Цернике и называемые по его имени «полиномы
Цернике».

Функция разложения волновой аберрации в ряд по полиномам Цернике выглядит следующим образом:

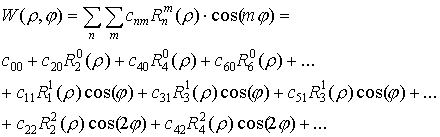(8.1.1)

где и — полярные координаты,
— степень , — степень ,
причем , () — четное число,
— радиальные полиномы Цернике, зависящие только от .

Полиномы Цернике ортогональны на окружности единичного радиуса. Условие ортогональности записывается так:

(8.1.2)

где — норма полинома.

Ортогональность полиномов Цернике дает им большие преимущества при анализе аберраций по сравнению со степенным базисом. Основными преимуществами являются:

абсолютные значения коэффициентов разложения по полиномам Цернике уменьшаются с увеличением степени полиномов, то есть ряд Цернике, как правило, всегда сходится, чего нельзя утверждать о степенном
ряде;
каждый коэффициент ряда дает вклад аберрации данного типа и порядка в общую волновую аберрацию с позиции взаимного баланса всех типов аберраций. Это означает, что отдельные типы аберраций, представленные
разложением по полиномам Цернике, влияют на качество изображения совершенно независимо друг от друга.

Кроме указанных преимуществ, полиномы Цернике образуют очень устойчивый базис к погрешностям вычислений при моделировании работы оптических систем на компьютере или математической
обработке результатов измерений. Поэтому полиномы Цернике используют для представления формы как в проектировании оптических систем,
так и в процедурах контроля качества изготовленных оптических систем и отдельных деталей.

8.1.2. Основные типы аберраций, представленные полиномами Цернике

Каждое слагаемое ряда () описывает
аберрацию определенного вида и порядка. В таблице приведены названия наиболее
важных компонентов разложения по полиномам Цернике. Все значения волновой и
аберраций даны для .

Таблица 8.1.1. Основные типы аберраций, представлнные полиномами Цернике

тип аберрации	профиль волнового фронта	поперечные аберрации	точечная диаграмма

3-го порядка
сферическая аберрация 5-го порядка
поперечное смещение ()
3-го порядка
кома 5-го порядка
3-го порядка			сагиттальный фокус меридиональный фокус в плоскости идеального изображения
астигматизм 5-го порядка