Как начиналась геометрия

Литература

• Александров А. Д., Нецветаев Н. Ю. Геометрия, — Наука, Москва, 1990.
• Александров П. С. Что такое неэвклидова геометрия, — УРСС, Москва, 2007.
• Делоне Б. Н. Элементарное доказательство непротиворечивости планиметрии Лобачевского, — Гостехиздат, Москва, 1956.
• Иовлев Н. Н. «Введение в элементарную геометрию и тригонометрию Лобачевского» . — М.-Л.: Гиз., 1930. — С. 67.
• Клейн Ф. «Неевклидова геометрия» . — М.-Л.: ОНТИ, 1936. — С. 356.
• Попов А. Г.

Лобачевского геометрия — геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.
Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Лобачевского геометрия вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Лобачевского геометрия имеет вполне реальный смысл. Лобачевского геометрия была создана и развита Н. И. Лобачевским, который впервые сообщил о ней в 1826. Лобачевского геометрия называется неевклидовой геометрией, хотя обычно термину «неевклидова геометрия» придают более широкий смысл, включая сюда и др. теории, возникшие вслед за Лобачевского геометрия и также основанные на изменении основных посылок евклидовой геометрии. Лобачевского геометрия называется специально гиперболической неевклидовой геометрией (в противоположность эллиптической геометрии Римана).

Лобачевского геометрия представляет теорию, богатую содержанием и имеющую применение как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще (см. Геометрия). С современной точки зрения можно дать, например, следующее определение Лобачевского геометрия на плоскости: она есть не что иное, как геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым образом. Именно, будем рассматривать круг на обычной плоскости (рис. 1) и внутренность его, т. е. круг, за исключением ограничивающей его окружности, назовем «плоскостью». Точкой «плоскости» будет точка внутри круга. «Прямой» будем называть любую хорду (например, а, b, b`, MN) (с исключенными концами, т. к. окружность круга исключена из «плоскости»). «Движением» назовем любое преобразование круга самого в себя, которое переводит хорды в хорды.

Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому Лобачевского геометрия Иными словами, всякое утверждение Лобачевского геометрия на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, т. к. через точку О, не лежащую на данной хорде а (т. е. «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b`). Аналогично, Лобачевского геометрия в пространстве может быть определена как геометрия внутри шара, выраженная в соответствующих терминах («прямые» — хорды, «плоскости» — плоские сечения внутренности шара, «равные» фигуры — те, которые переводятся одна в другую преобразованиями, переводящими шар сам в себя и хорды в хорды). Таким образом, Лобачевского геометрия имеет совершенно реальный смысл и столь же непротиворечива, как геометрия Евклида. Описание одних и тех же фактов в разных терминах или, напротив, описание разных фактов в одних и тех же терминах представляет характерную черту математики. Она ясно выступает, например, когда одна и та же линия задаётся в разных координатах разными уравнениями или, напротив, одно и то же уравнение в разных координатах представляет различные линии.

Факт 2. Ноль — это четное число

Одни скажут, что это знание уровня школы, но для других это совсем не то, о чем они когда-либо думали.

«Каждый год я предлагаю своим первокурсникам определенный набор вопросов, чтобы заставить их размять мозги, — рассказывает Стивен. — Это один из них, ведь он заставляет усомниться в самом определении четного числа. Я всегда получаю одни и те же результаты: все в аудитории утверждают, будто они знают, что такое четное число, но лишь немногие готовы встать и ответить, что ноль — одно из них».

Для ясности, грамотное определение четного числа звучит следующим образом: число считается четным, если при делении на 2 оно остается целым. Ноль подходит под это правило, ведь 0 : 2 = 0.

Интересные факты о цифрах занимательная математика. 10 обалденных фактов о математике, которые понравятся даже гуманитариям (2 фото)

даже гуманитариям 1. Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.

2. Религиозные евреи стараются избегать христианской символики и вообще знаков, похожих на крест. Например, ученики некоторых израильских школ вместо знака «плюс» пишут знак, повторяющий перевёрнутую букву «т».3. Подлинность купюры евро можно проверить по её серийному номеру буквы и одиннадцати цифр. Нужно заменить букву на её порядковый номер в английском алфавите, сложить это число с остальными, затем складывать цифры результата, пока не получим одну цифру. Если эта цифра — 8, то купюра подлинная.Ещё один способ проверки заключается в подобном складывании цифр, но без буквы. Результат из одной буквы и цифры должен соответствовать определённой стране, так как евро печатают в разных странах. Например, для Германии это X2.4. Бытует мнение, что Альфред Нобель не включил математику в список дисциплин своей премии из-за того, что его жена изменила ему с математиком. На самом деле Нобель никогда не был женат. Настоящая причина игнорирования математики Нобелем неизвестна, но есть несколько предположений. Например, на тот момент уже существовала премия по математике от шведского короля. Другое — математики не делают важных изобретений для человечества, так как эта наука имеет чисто теоретический характер.5. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса a с центрами в вершинах равностороннего треугольника со стороной a. Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия (с неточностью в 2%).

6. В русской математической литературе ноль не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.7. Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.8. Сумма всех чисел на рулетке в казино равняется «числу зверя» — 666.9. Софья Ковалевская познакомилась с математикой в раннем детстве, когда на её комнату не хватило обоев, вместо которых были наклеены листы с лекциями Остроградского о дифференциальном и интегральном исчислении.10. В штате Индиана в 1897 году был выпущен билль, законодательно устанавливающий значение числа Пи равным 3,2. Данный билль не стал законом благодаря своевременному вмешательству профессора университета.

Многие известные люди прошлого являлись и математиками в том числе

Все знают писателя Льюиса Кэролла, но почти никто не знаком с математиком Чарльзом Лютвиджом Додсоном. На самом же деле это один и тот же человек. Многие писатели были вовлечены не только в искусство, но и в точные науки. Также и Михаил Юрьевич Лермонтов. Помимо писательства он увлекался в свободное время решением математических задач.

Наполеон

Математика не оставляла равнодушными и полководцев. Наполеон был умным человеком, талантливым стратегом, скорее всего, вследствие этого он увлекался точными науками и оставил после себя несколько математических трудов. Вот они, интересные факты из жизни математиков, которые прославились совсем в других ролях!

Платон

Платон, живший в 428348 годах до нашей эры, считается, и, должно быть, справедливо я не специалист одним из величайших философов Греции.

Геометрия ко времени Платона уже была очень развита. Было решено много весьма и весьма сложных задач, доказаны сложнейшие теоремы. Но ясной позиции во взглядах на общую схему построения науки ещё не было. Развитие геометрии, как нередко бывает в науке, стимулировалось задачами, решения которых никак не удавалось отыскать. Требовалось при помощи циркуля и линейки, не привлекая никаких других геометрических инструментов:

• разделить данный угол на три равных части (трисекция угла);
• построить квадрат с площадью, равной площади данного круга (квадратура круга);
• построить куб с объёмом, в два раза большим объёма данного куба (делосская задача).

Только в конце прошлого века было доказано, что в такой постановке ни одна из этих задач не может быть решена, хотя, если использовать другие геометрические инструменты или (что то же) использовать при построении геометрические места точек, отличные от прямой либо дуги окружности, то все три задачи легко решаются.

Однако принятые у греков правила игры не позволяли пользоваться при решении задач ничем, кроме циркуля и линейки. Платон даже обосновал это ссылкой на авторитет богов.

Так что ни одна из проблем решена не была, но по ходу дела геометрия была основательно разработана.

Я с великим сожалением опускаю все анекдоты, связанные с этими задачами. Историй много, и все они прелестны, но нельзя слишком отвлекаться. Вспомню лишь одно из преданий, связанное именно с Платоном и показывающее его с лучшей стороны.

Однажды, рассказывает Эратосфен, на острове Делосе вспыхнула эпидемия чумы. Жители острова, естественно, обратились к Дельфийскому оракулу, который повелел удвоить объём золотого кубического жертвенника Аполлону, не изменяя его формы. За советом обратились к Платону. Платон задачи не решил, но зато истолковал оракула в том смысле, что боги гневаются на греков за нескончаемые междоусобные войны и желают, чтобы они, греки, вместо кровавых побоищ занимались бы науками и особенно геометрией. Тогда чума исчезнет.

Платон очень много сделал для развития математики и весьма ценил её. На входе в его академию был даже высечен весьма категорический лозунг: «Да не войдёт сюда тот, кто не знает геометрии». Дело в том, что Платон полагал: «Изучение геометрии приближает к бессмертным богам» и воспитывал в этом духе своих учеников, приплетая математику к месту и не к месту.

По-видимому, Платон первый чётко потребовал: математика вообще и геометрия в частности должны быть построены дедуктивным образом. Иначе говоря, все утверждения (теоремы) должны строго логически выводиться из небольшого числа основных положений аксиом. Такая постановка крупнейший шаг вперёд.

Некоторые из учеников Платона выросли в блестящих геометров. Но надо сказать, что и по своим взглядам, и по методам организации школы, и по любви к саморекламе Платон очень напоминает Пифагора.

На мой взгляд, как философ и как человек, Платон довольно несимпатичен. Во всяком случае, созданная им теория идеального государства, образцом которого послужила реальная и вполне фашистская страна Спарта восторга, мягко говоря, не вызывает. Основные положения его утопии в общем удовлетворяют требованиям нацистов. Всю свою жизнь он яростно боролся против демократии в политической жизни и против материализма в духовной. Философов-материалистов Платон не только абстрактно поносил в своих философских сочинениях, но, демонстрируя неплохую практическую хватку, нередко дискутировал, как сказали бы теперь, «в жанре политического доноса».

Приведу пример. Был в те времена в Греции замечательный философ, один из первых материалистов Анаксагор. (Мы почти ничего не знаем о его геометрических работах; известно, однако, что в темнице, где ему пришлось сидеть за свои взгляды, он исследовал проблему квадратуры круга.)

И вот Платон в одном из сочинений в диалоге жителя Афин (рупор самого Платона) и спартанца так расправляется с Анаксагором.

Афинянин: «Когда мы, стремясь получить доказательства существования богов, ссылаемся на Солнце, Луну, Звёзды и Землю как на божественные существа, то ученики этих новых мудрецов возражают нам, что всё это ведь только земля и камни, и они (т.е. камни) совершенно не в состоянии заботиться о людских делах».

Спартанец молниеносно чует ересь и возмущённо восклицает: «Какой же вред для семьи и государства проистекает от таких настроений у молодёжи!».

Так дискутировал Платон.

Сумма кубов

В теории чисел существует любопытная связь между суммой последовательных кубов набора натуральных чисел и квадратом суммы соответствующих чисел. Выглядит это следующим образом:

\(1^3+2^3+\dots+n^3=(1+2+\dots+n)^2\)

У этого, казалось бы, сугубо алгебраического факта помимо индуктивного доказательства есть еще и хорошее визуальное. Давайте покажем, как равенство работает на примере \(n=5\).

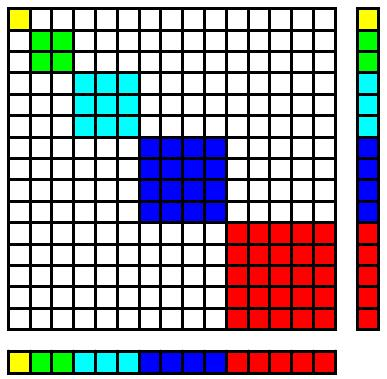
Перед вами квадрат площадью \(15\) на \(15\), где каждое число от \(1\) до \(5\) обозначено определенным цветом на каждой стороне (\(1\) – желтый квадрат, \(2\) – два зеленых, \(3\) – три бирюзовых квадрата и так далее). Очевидно, что площадь большого квадрата равна \((1+2+3+4+5)^2\). Неучтенные маленькие белые квадраты могут быть преобразованы в новые квадраты, а два прямоугольника могут быть преобразованы в квадраты так, как показано на рисунке ниже.

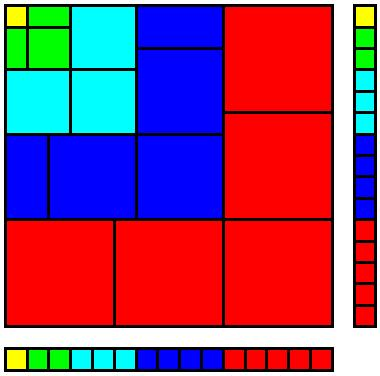
Таким образом, площадь всего квадрата равна сумме площадей красных квадратов – \(5^2 \cdot 5\), синих квадратов – \(4^2 \cdot 4\), голубых квадратов – \(3^2 \cdot 3\), зеленых – \(2^2 \cdot 2\) и наконец желтого квадрата – \(1^2 \cdot 1\). Тогда имеем следующее уравнение:\\ А выражение слева и есть сумма кубов. Для других значений \(n\) доказательство аналогичное.

Отцы-основатели

За многие тысячелетия огромное количество учёных занимались развитием математических знаний

Кто-то из них снискал себе мировую славу, кто-то оказался не столь известен широкой публике, но тем не менее, сделал в математике что-то весьма важное. Список известных математиков состоит из многих десятков, если не сотен, фамилий. Мы упомянем лишь некоторых: тех, кто волею судьбы или благодаря своей гениальности оказался «на исторической сцене»

И начнём с нескольких имён тех людей, кто жил и творил в глубокой древности, но заложил, таким образом, основы этой науки

Мы упомянем лишь некоторых: тех, кто волею судьбы или благодаря своей гениальности оказался «на исторической сцене». И начнём с нескольких имён тех людей, кто жил и творил в глубокой древности, но заложил, таким образом, основы этой науки.

Эвклид

Этот учёный из Древней Греции жил примерно в III веке до нашей эры. Примерно, потому что мы мало знаем о его жизни, разве лишь то, что проживал он в Александрии. Да и то, некоторые источники, особенно арабские, утверждают, что на самом деле Эвклид был «прописан» в Дамаске.

Эвклида называют отцом геометрии. Он доказал много теорем и гипотез, написал несколько научных трактатов. Из них два труда — «Элементы» и «Начала», заложили базовый фундамент всей последующей европейской математики. В «Началах» содержится известная каждому школьнику теорема Пифагора. По этому учебнику преподавали геометрию в школах Европы около 2 тысяч лет!

Пифагор

Если Эвклид — отец геометрии, то Пифагора величают отцом математики. Он также жил в Греции, за полторы сотни лет до Эвклида. Создал собственную математическую школу, впервые в истории человечества сделал математику прикладной наукой, вводя её элементы в повседневный обиход. Кстати, далеко не все историки согласны с тем, что именно он доказал свою знаменитую тригонометрическую теорему.

Архимед

Древнегреческий учёный из Сиракуз занимался многими науками, но, по словам Плутарха, «был одержим математикой». Много работал в области геометрии, сам же считал своим главным достижением выведение формулы для исчисления площади шара и его объёма. Идеи Архимеда заложили основу интегрального исчисления.

«Начала»

Повторюсь эта книга уникальна. Более двух тысяч лет она была главным и практически единственным руководством по геометрии для учёных как западного, так и восточного мира. Ещё в конце XIX столетия во многих английских школах геометрию изучали по адаптированному изданию «Начал», и вряд ли можно найти более выразительное свидетельство популярности. В этом смысле конкурировать с «Началами» могут разве что Библия и Евангелие.

Но, в отличие от них, основа «Начал» строгая и жёсткая логика, точнее, Евклид всё время стремится к таковой. Можно полагать, что он был последователем Платона и Аристотеля. А Платон, как вы помните, требовал строго дедуктивного построения математики.

В фундаменте аксиомы, основные положения, принимаемые без доказательства, а далее всё должно быть строго логично выведено из аксиом. Этот идеал и пытается осуществить Евклид.

С современных позиций буквально вся его аксиоматика неудовлетворительна. Но это легко заявлять сейчас, после 25 веков исследований. А в своё время логика Евклида оставляла совершенно подавляющее впечатление. Во всяком случае, не следует забывать, что сама логическая схема её стала с тех пор канонической для построения любого раздела математики.

Попытки изложить геометрию на основе аксиоматического метода были и до Евклида. Но можно уверенно заключить, что работа Евклида была наиболее удачной. Свидетельство тому необычайная известность его книги уже в древнем мире, благодаря которой она и дошла до нас.

«Начала» блестяще написаны, в них чувствуется мастер своего дела, тонкий учёный и великолепный педагог. Поэтому поголовное поклонение математиков Евклиду и его «Началам» понятно и оправданно. Добавим ещё, что эта книга обратила в математическую веру несколько десятков молодых людей, ставших впоследствии крупнейшими математиками мира.

Влияние Евклида было поразительно во все века во всех краях света. Вот, например, в каких восхищённых тонах говорил о «Началах» один из виднейших математиков эпохи Возрождения Кардано: «Неоспоримая крепость их догматов и их совершенство настолько абсолютны, что по-видимому, только тот способен отличать в сложных вопросах геометрии истинное от ложного, кто усвоил Евклида».

А вот слова неизвестного английского геометра (это уже середина XIX века): «Никогда не было системы геометрии, которая в существенных чертах отличалась бы от плана Евклида; и до тех пор, пока я не увижу этого собственными глазами, я не поверю, что такая система может существовать».

Приведу одно яркое свидетельство влияния «Начал» буквально на все области мышления. Один из крупнейших в истории Западного мира философов, замечательный не только как философ, но и как человек Спиноза весь план своего основного сочинения «Этика» целиком заимствовал у Евклида.

И, наконец, для тех, кого не убеждает пример Спинозы, я приберёг Ньютона. Его основополагающий труд «Математические начала натуральной философии» копирует не только заглавие книги Евклида, но и её построение: великий Ньютон тоже выводит все свои результаты из набора аксиом!

Из истории математики

Самым древним математическим трудом можно назвать записи, найденные в Свазиленде на кости бабуина, сделанные путем выбивания чёрточек (кость из Лембобо). Предположительно, на поверхности этой кости размещены результаты какого-то вычисления. Кость датируется возрастом в 37 000 лет.

На территории современной Франции, археологами был обнаружен ещё более сложные математические расчеты – волчья кость, на которой выбиты чёрточки, сгруппированные по пять штук. Возраст кости составляет примерно 30 000 лет.

кость из Ишанго (Конго)

На знаменитой кости из Ишанго (Конго) выбита группа простых чисел. Полагают, что вычисления на ней были сделаны примерно 18-20 тысяч лет назад.

Вавилонская табличка с числами Пифагора

Самым древнейшим математическим текстом считается вавилонская табличка с кодовым названием «Plimpton 322», которая были создана примерно в 1800-1900 году до нашей эры. На ней изображена таблица, состоящая из 4 столбцов и 15 строк чисел, записанных клинописью того периода. Как оказалось, таблица содержит список пифагоровых чисел, то есть чисел, которые являются частным решением теоремы Пифагора, к примеру: 3, 4, 5.

Человеческие пальцы — основной инструмент для счёта древних

Десятеричная система счисления используется человечеством по причине того, что мы имеем по десять пальцев на руках. Использовать для счёта именно пальцы рук оказалось удобнее всего.

Такая цивилизация как майя, а также чукчи использовали двадцатеричную систему счисления, используя для счёта не только пальцы рук, но и ног.

Основой для двенадцатеричной и шестидесятеричной систем в древних Шумере и Вавилоне тоже послужили человеческие руки. При помощи большого пальца отсчитывали фаланги остальных пальцев ладони, число которых составляет 12.

В часах используется шестидесятеричная система счисления

Древние вавилоняне делали вычисления, основанные на шестидесятеричной системе счисления, вместо нынешней десятичной. Именно поэтому у нас 60 секунд в минуту и 360 градусов по кругу.

До 1900 года результаты всех основных мировых математических исследований можно было уместить в 80 учебниках. В нынешнее время все математические доказательства с трудом уместятся в 100 000 книгах.

Знак равенства

Современный знак равенства «=» впервые был применён англичанином Робертом Рекордом в 1557 году.

Ортодоксально настроенные евреи тщательно избегают христианской символики и вообще знаков, схожих с крестом. К примеру, ученики ряда ортодоксальных израильских школ вместо знака «+» пишут символ, похожий на перевёрнутую букву «т».

Математический институт Клэя обещает выплатить 1000 000 долларов тому, кто решит хотя бы одну из гипотез: гипотеза Ходжа и гипотеза Римана.

Пузырь знаний

Американские исследователи заявляют, что студенты, которые жуют жвачку во время прохождения теста по математике, достигают более лучших результатов.

В математике существуют разные интересные названия её разделов: теория игр, теория кос и теория узлов.

Известный труд Исаака Ньютона под названием «Математические начала натуральной философии» содержит простейшие ошибки вычислений, которые оставались незамеченными на протяжении свыше 300 лет.

Закон Бенфорда утверждает, что распределение первых цифр в числах некоторого наборов данных из реального мира неравномерен. К примеру цифры от 5 до 9 встречаются гораздо реже на первых позициях, чем цифры от 1 до 4. Существует и практическое применение данного закона. Оно заключается в том, что по нему можно проверять достоверность бухгалтерской и финансовой отчетности, результатов голосований и многое другое.

Гамбургер от A&W

Провалом закончилась крупная рекламная кампания 1980-х годов сети быстрого питания A&W. В отличие от аналогичного сэндвича, весом в 1/4 фунта, из известного Макдоналдса, гамбургер производства A&W весил треть фунта и при этом стоил дешевле. Также покупатели отмечали, что он по вкусовым качествам лучше. По данным исследования, впоследствии проведенной самой компанией главной причиной неуспеха явилось банальное незнание американцами математики. Большое количество потенциальных клиентов попросту не понимало значения дробных чисел. Предложение им показалось не выгодным, поскольку 3 меньше 4.

Следующее предложение верно, но вы не должны верить этому. Предыдущее предложение было ложным.

Человечество привыкло завязывать галстуки всего с помощью нескольких способов. Математиками подсчитано, что всего существует 177 147 способов его завязать.

Математические числа люди тесно связывают с мистикой

Для многих людей, особенно в Средние века, и в более раннее время, числа носили характер не просто средств для решения задач или бытовых вычислений, а могли быть, например, счастливыми или несчастливыми. Число 13 на Руси называлось «чертовой дюжиной» и вследствие библейских поверий считалось несчастливым, в то время как число 7 многие люди по всему миру считают приносящим удачу.

интересный факт о математике

Но так называемым «лидером» по приписываемым ему мистическим свойствам является число 666. Интересно, что 666 – это сумма всех чисел на рулетке казино. Данное число хоть и используется в повседневной жизни, но многие люди все равно считают его нехорошим. Например, в Европарламенте есть кресло под номером 666, но по традиции оно никем не занимается. Интересные факты, связанные с математикой, окружают нас повсюду.

Теорема Пифагора

«Квадрат гипотенузы равен сумме квадратов двух катетов», – гласит известная теорема Пифагора, знакомая каждому со школьной скамьи. Был ли Пифагор первым, кто доказал эту теорему, нельзя утверждать наверняка. Существует как минимум \(114\) самых разнообразных подходов к доказательству этой теоремы. Так индийский математик Бхаскара (ок. \(1114\)-\(1185\) г.) доказал теорему Пифагора, просто нарисовав эту картинку и сказав: «Вот!»

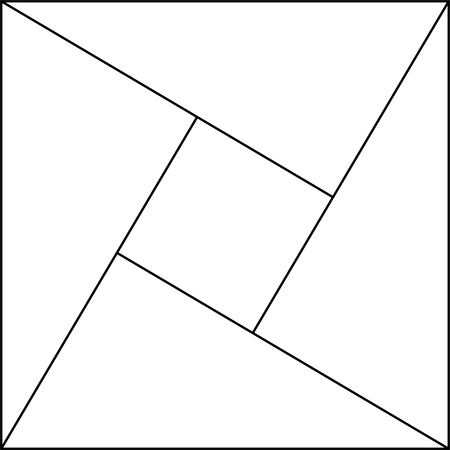
Среди древних индийских математиков практика словесного доказательства не пользовалась особой популярностью – они любили визуальные. Именно в древней Индии, как предполагают ученые, зародились первые понятия визуальных доказательств.

Прежде чем пускаться в визуальное доказательство теоремы Пифагора, предложенной Бхаскара, давайте для начала обозначим стороны прямоугольного треугольника \(a, b, c\) так, как показано на рисунке, а затем рассмотрим площадь всей фигуры.

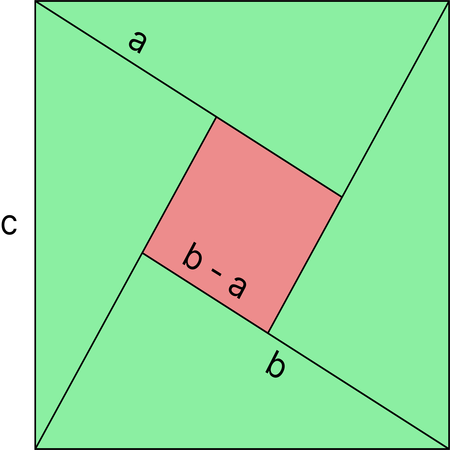
С одной стороны, она равна площади большого квадрата – \(c^2\). С другой стороны, она равна площади всех составляющих ее фигур, т. е. сумме площадей четырёх треугольников и маленького квадратика. Вычислим площадь каждого треугольника по уже известной формуле: \(\frac{a\cdot b}{2}\). Тогда площадь всех четырех треугольников будет \(4 \cdot \frac{ab}{2} = 2 ab\). Не сложно заметить, что сторона маленького квадратика в центре равна \(b — a\). Следовательно, его площадь – \((b-a)^2\). Из всего этого выходит, что площадь большого квадрата равна \(2ab+(b-a)^2 = a^2 + b^2\). Теорема доказана.

P. S. Использованный нами метод называется подсчетом двумя способами и знаком многим олимпиадникам по математике!

Программисты и часы

— Доброе утро. Который сейчас час?

— Сложи 1/4 времени, прошедшего с полуночи до сейчас, с 1/2 от сейчас до полуночи.

— Спасибо, я понял.

— Не сомневался.

Вопрос: который час?

На самом деле это очень простая задача, если помнить, что в сутках 24 часа.

Пусть от полуночи до сейчас прошло Х времени. Тогда от сейчас до полуночи осталось 24 – Х времени.

С другой стороны, если мы сложим четверть времени от полуночи до сейчас и половину времени от сейчас до полуночи, то как раз получим Х — время, которое сейчас:

(¼ × Х) + (½ × (24 − Х)) = Х

Раскрываем скобки:

Х/4 + 12 − Х/2 = Х

Перенесём все Х в одну сторону, а 12 — в другую:

Х − Х/4 + Х/2 = 12

Х + Х/4 = 12

5Х/4 = 12

5Х = 48

Х = 9,6

Получается, что с полуночи прошло 9,6 часа, или 9 часов 36 минут.

Ответ: на часах 9:36.

Фрактал

Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.

При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).

Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.

О числах

• В переводе с арабского слово «цифра» означает «ноль», но так исторически сложилось, что сейчас этим словом называют все цифры.
• 666 — самое мистическое и окутанное легендами число. Сумма всех чисел игровой рулетки равна 666, а в Европарламенте есть кресло с этим номером, но по давней традиции на него никто не садится.
• Китайцы не любят использовать цифру 4, т.к. на их языке она произносится как «смерть».

• Вплоть до 19 века отрицательные числа практически не использовались, пока их не ввел в привычный оборот итальянский купец Пизано, чтобы фиксировать свои долги.
• В тайском языке число 5 произносится как «ха», а 555 — это сленговая фраза, обозначающая смех.
• Итальянцы не любят число 17, т.к. еще в Древнем Риме на надгробиях писали фразу «меня больше нет», которая визуально выглядела как VIXI (цифры 6 и 11, сумма которых равна 17).

Применение математики в жизни человека

Помимо того, что постулаты этой фундаментальной науки используют в своей работе ученые и изобретатели, люди других профессий, не связанных с наукой, тоже нередко прибегают к математическим расчетам в обычной жизни.

Например, заправляя авто, мы умножаем стоимость литра бензина на нужный объем и получаем ту сумму, которую нужно будет заплатить. Совершая покупки в магазине, подсчитывая хватит ли денег в кошельке или на счету банковской карты, мы начинаем оценивать общую стоимость товаров, складывая их цены.

Делая ремонт в доме, мы высчитываем площадь стен исходя из их ширины и высоты, чтобы знать, сколько рулонов обоев купить.

Решив приумножить свой доход, мы оцениваем выгоду по вкладам в том или ином банке, рассчитываем, сколько получим прибыли в денежном выражении, если оформим вклад под 7%, а если под 8,5%. Решив же взять кредит, каждый человек оценивает, сколько ему придется переплатить и стоит ли оно того.

Для всего этого нужно хотя бы минимальные математические знания.

Чтобы сжечь одну килокалорию, нужно нажать кнопку мышки 10 миллионов раз

Как-то дочь учителя физики начала утверждать, что каждый раз, когда человек нажимает кнопку компьютерной мыши, он сжигает одну килокалорию. Учитель из Луизианы, отнесясь к этому скептически, сделал расчет, высчитав, сколько на самом деле нужно нажать на кнопку мыши, чтобы сжечь 1 килокалорию.  

При условии, что для нажатия кнопки мыши требуется сила в 0.5 ньютонов, а расстояние перемещения кнопки принять за 1 миллиметр, то в среднем для того, чтобы сжечь одну килокалорию, потребуется нажать кнопку около 10 миллионов раз (10 ^- 5 джоулей, или 10 ^- 7 килокалорий). Кстати, это займет всего 11,5 дней. Так что принимайтесь за работу! 

Математические гении и их открытия

Одним из самых известных математических гениев был Архимед, живший в III веке до нашей эры. Он считается отцом математического анализа и разрабатывал методы исчисления площадей и объемов. Его открытия исследуются и используются до сих пор в науке и технике.

Другой знаменитый математический гений — Эйлер, живший в XVIII веке. Он внес огромный вклад в различные области математики, включая теорию чисел, теорию функций и геометрию. Он также разработал множество математических методов и нотаций, которые используются по сей день.

Еще одним из великих математических гениев был Карл Фридрих Гаусс. Он считается одним из самых влиятельных математиков всех времен. Он внес огромный вклад в теорию чисел, алгебру и геодезию. Гауссом была открыта теорема Гаусса-Муро, а также разработан метод минимумов квадратов.

Это лишь некоторые из математических гениев и их открытий, которые помогли сформировать современную математику. Их работа и вклад в науку невозможно переоценить, именно они легли в основу многих современных математических теорий и приложений.