В чем отличие между понятиями «число» и «цифра»?

Десятичные дроби

Поскольку человечество все больше использовало десятичную систему счисления, то для приведения записей дробных чисел к десятичному виду, дроби со знаменателями в виде разрядных единиц 10, 100, 1000, 10 000 и т.д. начали записывать в виде десятичных дробей, где дробная часть отделялась от целой запятой или точкой. Например, 1/10 = 0.1, 1/100 = 0.01, 1/1000 = 0.001, 1/10000 = 0.0001. Более того, обычные дроби стали переводить в десятичный вид делением числителя на знаменатель и если точная замена не удавалась, то производилась приблизительно, с удовлетворяющей практические потребности людей точностью.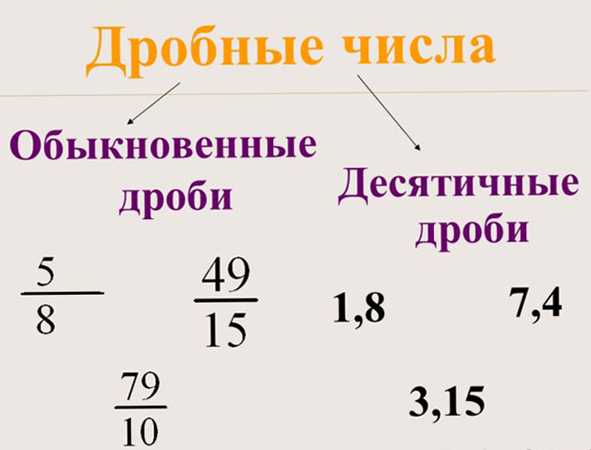

Не надо думать, что привычная нам десятичная система счисления, с десятью цифрами, использовалась всегда и везде. Например, в знаменитой Римской империи использовались совсем другие цифры, которые и сейчас иногда используются для нумерации глав в книгах, обозначения столетий и т.п. Эти цифры мы называем римскими и было их всего семь: І – один, V – пять, Х – десять, L – пятьдесят, С – сто, D – пятьсот, М – тысяча. С помощью этих семи цифр и записывались все остальные числа. Если меньшая цифра стояла перед большей, то она вычиталась из большей, а если после большей, то прибавлялась к ней. Некоторые одинаковые цифры могут повторятся не более трех раз подряд. Например, II – два, III – три, IV – четыре (5 – 1 = 4), VI – шесть (5 + 1 = 6).

Таблица названий больших чисел, разрядов и классов

1-й класс единицы	1-й разряд единицы 2-й разряд десятки 3-й разряд сотни	1 = 10 0 10 = 10 1 100 = 10 2
2-й класс тысячи	1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч	1 000 = 10 3 10 000 = 10 4 100 000 = 10 5
3-й класс миллионы	1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов	1 000 000 = 10 6 10 000 000 = 10 7 100 000 000 = 10 8
4-й класс миллиарды	1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов	1 000 000 000 = 10 9 10 000 000 000 = 10 10 100 000 000 000 = 10 11
5-й класс триллионы	1-й разряд единицы триллионов 2-й разряд десятки триллионов 3-й разряд сотни триллионов	1 000 000 000 000 = 10 12 10 000 000 000 000 = 10 13 100 000 000 000 000 = 10 14
6-й класс квадриллионы	1-й разряд единицы квадриллионов 2-й разряд десятки квадриллионов 3-й разряд десятки квадриллионов	1 000 000 000 000 000 = 10 15 10 000 000 000 000 000 = 10 16 100 000 000 000 000 000 = 10 17
7-й класс квинтиллионы	1-й разряд единицы квинтиллионов 2-й разряд десятки квинтиллионов 3-й разряд сотни квинтиллионов	1 000 000 000 000 000 000 = 10 18 10 000 000 000 000 000 000 = 10 19 100 000 000 000 000 000 000 = 10 20
8-й класс секстиллионы	1-й разряд единицы секстиллионов 2-й разряд десятки секстиллионов 3-й разряд сотни секстиллионов	1 000 000 000 000 000 000 000 = 10 21 10 000 000 000 000 000 000 000 = 10 22 1 00 000 000 000 000 000 000 000 = 10 23
9-й класс септиллионы	1-й разряд единицы септиллионов 2-й разряд десятки септиллионов 3-й разряд сотни септиллионов	1 000 000 000 000 000 000 000 000 = 10 24 10 000 000 000 000 000 000 000 000 = 10 25 100 000 000 000 000 000 000 000 000 = 10 26
10-й класс октиллион	1-й разряд единицы октиллионов 2-й разряд десятки октиллионов 3-й разряд сотни октиллионов	1 000 000 000 000 000 000 000 000 000 = 10 27 10 000 000 000 000 000 000 000 000 000 = 10 28 100 000 000 000 000 000 000 000 000 000 = 10 29

Невозможно представить себе жизнь без счёта. В обиходе каждый из нас встречает и цифры, и числа ежедневно, даже не задумываясь, где работает с цифрами, а где с числами, и в чём их отличие.

Определение цифры следующее: знак, принятый и используемый для обозначения количества (выраженного в числовом эквиваленте). А число – это выражение количественных характеристик в удобном виде, посредством цифр. Отсюда два вывода: числа состоят из цифр и цифра обладает знаковыми свойствами (обусловленность, узнаваемость, неизменяемость, и т.д.). Числа также обладают знаковыми свойствами, так как это некая абстракция, однако они обладают ими лишь потому, что состоят из цифр. Но цифра не только используется нами, как составляющее числа, но и как самостоятельный аналог числа, если речь идёт о предметах в количестве от одного до девяти включительно (так как цифр 10 – от нуля до девяти). Данные признаки применимы не только к арабским цифрам, но и к римским. Аналогично I V X L C D M – это римские цифры, а вот V I I I – это римское число, хотя понятийно в другой системе счисления ему соответствует арабская цифра 8.

Гипотезы

Сегодня нет однозначного мнения насчет формирования написания арабских цифр. Ни один ученый не знает, почему определенные цифры выглядят именно таким образом, а не как-то по-другому. Чем руководствовались древние ученые, придавая цифрам формы? Одной из самых правдоподобных гипотез является та самая, с количеством углов.

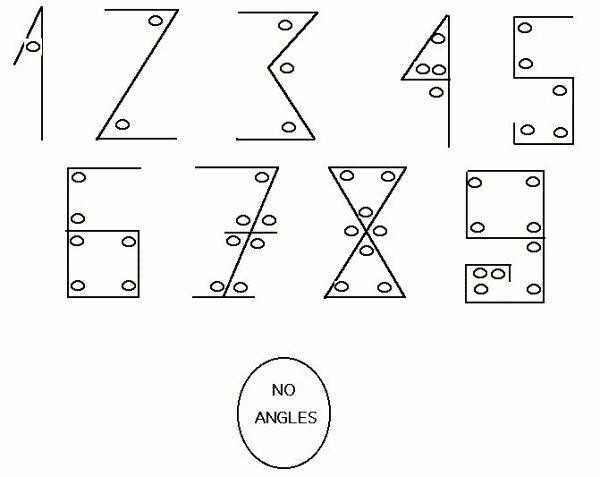
Конечно, с течением времени все углы у цифр сглаживались, они постепенно приобрели привычный для современного человека облик. И уже огромное число лет арабские цифры по всему миру используются для обозначения чисел. Удивительно, что всего десятью символами можно передать невообразимо большие значения.

Как дать характеристику числу?

Разберём несколько примеров.

Число 7 — однозначное, нечетное, соседи числа 7 числа 6 и 8.

Также чисел первого десятка можно добавить такое дополнительное задание, как состав числа. Т.е. число 7 можно получить сложением чисел 1 и 6, 2 и 5, 3 и 4.

Число 10 — двузначное, чётное, круглое, соседи числа 9 и 11. Число 10 можно получить сложением чисел 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5.

Чем крупнее число, тем больше можно о нём рассказать.

Число 999 — наибольшее трёхзначное число, нечётное, соседи 998 и 1000, в числе 9 сотен, 9 десятков и 9 единиц.

Надеюсь, что полученные знания были вам полезны и теперь вы знаете чем отличается цифра от числа, сможете объяснить это ребёнку простыми словами, а также потренироваться давать характеристику числам.

Что такое число?

Мы узнали, что такое цифра, но понятие числа все еще неизвестно. Числа — это отвлеченные понятия, которые используются для численной функциональности каких-либо объектов. Они появились еще в обществе первобытных людей. Уже в те времена возникла потребность в счете. Со временем числа преобразовывались и дополнялись. В итоге они оказались первым математическим суждением. Какие же имеются числа?

• Натуральные. Их мы получаем при естественном счислении. Натуральные числа применяются нами ежедневно.
• Целые. Их мы получаем путем объединения натуральных чисел с множеством отрицательных чисел и с нулем. Они ограничены в сложении, вычитании и умножении, но не в делении.
• Рациональные. Они отображаются чаще всего в виде дроби. Для рациональных чисел характерны все четыре арифметические действия: сложение, умножение, вычитание и деление.
• Действительные — это множество рациональных чисел, которые делятся на алгебраические и трансцендентные.
• Комплексные. Они представлены расширением большого количества действительных чисел. Они находятся в обиходе при решении задач гидродинамики, теории упругости, квантовой механики.

Системы счисления

Система счисления – это некий вариант представления чисел.

К примеру, представьте, что перед вами лежит несколько яблок. Вы хотели бы узнать, сколько яблок лежат на столе? Для этого вы могли бы считать, загибая пальцы рук или делать зарубки на дереве. А могли бы вы и представить, что десять яблок – это одна корзинка, а одно яблоко – это одна спичка. Спички по ходу счета выкладывать на столе под одной.

В первом варианте подсчета число получилось в виде строки из зарубок на дереве (или загнутых пальцев рук), а во втором варианте подсчета – это был набор из корзинок и спичек. Слева должны быть емкости, а справа — спички.

Системы счисления бывают двух видов:

1. Позиционные.
2. Непозиционные.

Позиционные системы счисления бывают:

• Однородными.
• Смешанными.

Непозиционной называют такую систему счисления, в которой цифра в числе соотносится с такой величиной, которая не зависит от ее разряда. Поэтому, если у вас пять зарубок, то число будет равно пяти. Ибо каждой зарубке будет соответствовать одно яблоко.

Позиционной системой счисления является та, в которой цифра в числе будет зависеть от ее разряда.

Та система счисления, к которой мы привыкли – это десятичная система счета. Она позиционная.

Когда наши предки начали учиться считать, у них появилась идея записывать числа. изначально они использовали те самые зарубки на деревьях или камнях, где каждая черточка обозначала какой-либо предмет (одно яблоко, к примеру). Именно так и была изобретена единичная система счисления.

Что такое цифра?

Цифра — это упорядоченная знаковая система, предназначенная для записи чисел. Цифрами считаются только те символы, которые в отдельности обозначают числа. Например, знак «-» хоть и применяется для того, чтобы записать число, но цифрой он не считается. Цифрами считается ряд от 0 до 9. Само слово «цифра» имеет арабские корни и обозначает «ноль» или «пустое место». Эти символы бывают следующих видов:

Это перечислены самые известные разновидности. В разных языках, например, в древнегреческом, для записи чисел используют буквы. Чаще всего в обиходной речи люди под словом «цифры» подразумевают числа, которыми записываются числовые данные. Следует помнить, что отрицательных, дробных и натуральных цифр не существует.

Привычная нам система исчисления основывается на цифрах арабского происхождения, которые стали известны европейцам в 13-м веке. До этого для записи чисел использовали римские графические символы. Сейчас эту разновидность можно увидеть на циферблате часов, а также в книгах.

Число — это основное математическое понятие. Его используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

Числа записываются цифрами и иногда при помощи символов операций в математике. Они возникли еще в первобытном обществе, когда появилась потребность в счете. Числа бывают:

• натуральные — получаются при естественном счете;
• целые — получаются при помощи объединения натуральных чисел;
• рациональные — имеют вид дроби;
• действительные;
• комплексные.

Два последних вида чисел имеют важное значение для математического анализа и получаются благодаря расширению рациональных (для действительных) и действительных (для комплексных) чисел. Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

1. С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
2. Число может быть отрицательным, дробным, в отличие от цифр.
3. Количество цифр всего 10, а чисел — бесконечное множество, т.к. они состоят из цифр.

Кроме различий, с математической точки зрения, существуют и лингвистические отличия. Они рассматривают, в каких случаях можно говорить «цифра», а когда — «число». Если в разговоре упоминаются официальные показатели, то уместно говорить слово «цифра». Это могут быть, например, статистические данные.

Понятие «цифры» широко распространено в нумерологии. Нумерологи используют это понятие как знак, который способен влиять на судьбу человека. Они наделяют его мистическими свойствами. Например, нумерологи уверены в том, что некоторые цифры притягивают удачу.

Число употребляют тогда, когда нужно назвать количество чего-либо, или когда речь идет о календарной дате или дне месяца. В русском языке для употребления этого понятия применяются порядковые числительные.

По сравнению с первобытными и древними обществами, у понятия «цифра» расширилась область употребления. Теперь это — не только в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами — теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Всем людям с раннего детства знакомы цифры, с помощью которых ведется счет предметов. Их всего десять: от 0 до 9. Потому и система исчисления называется десятичной. С помощью них можно записать совершенно любое число.

Тысячелетиями люди применяли свои пальцы для обозначения чисел. Сегодня десятичная система используется повсюду: для измерения времени, при продаже и покупке чего-либо, при различных расчетах. Каждый человек имеет собственные числа, например, в паспорте, на кредитной карте.

Что правило нам расскажет?

Вспоминаем, как пишутся буквы «и», «ы» после согласной «ц».

А правило нам говорит, что гласная «И» пишется в корнях слов:

• Цистит.

• Цинга.

• Циркуль.

В словах с окончанием «ция»:

• Корпорация.

• Революция.

• Авиация.

Буква «ы» пишется в случае, если у нас есть суффикс «ын»:

• Сестрицын.

• Синицын.

В окончании существительных во множественном числе:

• Курицы.

• Улицы.

• Пепельницы.

А еще у нас есть слова-исключения, в их корнях всегда будет писаться буква «ы»:

Цыган, цыкнуть, цыц, цыпленок, цыпочки.

Возвращаясь к тому, как же правильно, писать — цыфра или цифра? Давайте хорошенько подумаем. Это слово входит в число слов-исключений? Нет. Оно стоит во множественном числе? Тоже нет. Это суффикс, оканчивающийся на «цын»? И этот вариант отпадает.

Значит что остается? Правописание гласной «и». Она, как мы выяснили, пишется в корнях слова. В нужном нам слове корень «цифр». Пишем цифра или цыфра? Разумеется, первый вариант, согласно правилам русского языка.

Чем отличается цифра от числа?

Таким образом, цифра – это просто знак, символ, который можно сравнить с буквами в словах. Число же является математическим понятием, количественным показателем, и для его графического изображения используются именно цифры. Рассматривая статистики, графики, отчеты – любые количественные данные, мы видим числа, а не цифры.

Цифры числовой системы майя с индийско-арабскими эквивалентами

Разнообразие чисел довольно большое. Они могут быть целыми, четными, нечетными, положительными, отрицательными и т.д. Также не существует какого-либо последнего числа – всегда будет то, что больше него. Количество цифр ограничено десятью знаками: от 0 до 9. Сравнивать между собой можно только числа, а не цифры.

По материалам: kipmu.ru

Что такое цифра?

Это вопрос, на который мы получаем ответ изначально от родителей, потом от преподавателей в учебных заведениях. Что такое цифра? А из словаря Владимира Даля можно узнать, что цифры — это численные показатели. Именно они представляются символами чисел. Нам известно всего 10 цифр: от нуля до девяти. Из их сочетания получается бесконечность чисел. Какие же существуют цифры?

• Арабские. Такими символами мы пользуемся довольно-таки давно. Они возникли в Европе еще в 10-м веке.
• Римские. Возникли еще за пять веков до нашей эры и находились в обиходе у племен этрусков, проживавших на Апеннинском полуострове.
• Цифры майя. Такие знаки использовались для расчетов в календаре.

Но в современном мире цифра — это не только математический знак, и сегодняшний день существует даже цифровое телевидение, а также существует цифровой формат.

Единичная система счисления

Различие между цифрой и числом в единичной системе счисления в том, что число в этом случае равнозначно строке, состоящей из палочек. Количество палочек (зарубок на дереве) равняется значению числа.

К примеру, урожай из 50 яблок будет равен числу, состоящему из 50 палочек (черточек, зарубок).

Сколько цифр содержит число 50? Две цифры. Цифра 0 и цифра 5. Но количество яблок гораздо больше двух.

Основное неудобство в этой системе счисления – слишком длинная строка из черточек. А если бы урожай составлял 5 000 яблок? Действительно, записывать такое число неудобно. Прочтение тоже будет вызывать затруднения.

Поэтому позже наши предки научились группировать черточки по несколько штук (по 5, 10). И для каждой объединяющей группы был придуман специальный знак. Сначала для 5 и 10 использовали пальцы рук. А затем были придуманы определенные символы. Таким способом считать яблоки стало гораздо проще.

Цифры

Цифры — это символы, которые используются для представления чисел в письменной форме. Цифры являются основными элементами, из которых состоят числа. Они представляют определенные значения и используются в математике, науке, технике и многих других областях.

Цифры — это абстрактные символы, которые представляют конкретные значения и служат инструментом для измерения, подсчета и описания количественных характеристик объектов и явлений. Цифры играют важную роль в математике и являются одной из ключевых концепций этой науки.

Использование цифр позволяет совершать различные математические операции, такие как сложение, вычитание, умножение и деление. Отношение между цифрами может быть представлено в виде пропорции или соотношения, которое позволяет выражать разные количественные свойства объектов и явлений.

Цифры могут быть записаны в различных системах счисления, таких как десятичная система, двоичная система и шестнадцатеричная система. В разных системах счисления цифрами могут быть разные символы, но их значение остается неизменным.

Основная разница между числами и цифрами заключается в том, что числа представляют собой абстрактные концепции, которые обозначают количество или порядковый номер объекта, тогда как цифры являются символами, которые представляют эти числа в письменной форме.

Определение и особенности цифр

Цифра в математике — это символ, используемый для представления числа. Цифры являются основными элементами числовой системы и используются для создания чисел и записи числовых значений.

Цифры образуют множество, известное как система счисления. Самая распространенная система счисления — десятичная, в которой используются цифры от 0 до 9. Однако существуют и другие системы счисления, такие как двоичная (использующая только цифры 0 и 1) и шестнадцатеричная (использующая цифры от 0 до 9 и символы от A до F).

Одна из особенностей цифр — их связь с числами. Цифра сама по себе не имеет числового значения, но при совмещении с другими цифрами она может создавать числа. Например, цифра 5 по себе не имеет значения, но когда она объединяется с другими цифрами, например, 57, она создает число пятьдесят семь.

Цифры также могут использоваться для создания пропорций и абстрактных отношений. Например, в десятичной системе счисления цифра 1 находится перед цифрой 2, которая находится перед цифрой 3 и т.д. Это указывает на возрастающую последовательность чисел.

Цифры являются фундаментальными элементами математики и широко используются в нашей повседневной жизни. Они помогают нам представлять числа, выполнять математические операции и коммуницировать числовую информацию.

Примеры использования цифр:

Цифры играют важную роль в мире математики. Они используются для представления чисел и выполнения различных операций. Цифры — это символы, которые представляют конкретные значения.

Вот несколько примеров использования цифр:

• Представление чисел: Цифры используются для представления чисел. Например, число «5» в математике представляется цифрой «5». Числа могут быть положительными, отрицательными, или дробными, и цифры помогают нам представить эти различные значения.
• Выполнение арифметических операций: Цифры используются для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и деление. Например, если у нас есть числа «2» и «3», мы можем использовать цифры «2» и «3» для выполнения операции сложения и получить результат «5».
• Пропорция и отношение: Цифры используются для представления пропорций и отношений. Например, если у нас есть пропорция «2:3» или отношение «2 к 3», мы используем цифры «2» и «3», чтобы указать соответствующую пропорцию или отношение.
• Различные системы счисления: Цифры используются для представления чисел в различных системах счисления. Например, в десятичной системе счисления мы используем цифры от «0» до «9» для представления чисел, а в двоичной системе счисления мы используем только две цифры — «0» и «1».

Цифры являются абстракциями, которые помогают нам понять суть математических концепций и операций. Они представляют числа и позволяют нам манипулировать ими для решения различных задач.

Числа

Цифра и число – два понятия, которые часто используются в повседневной жизни и в математике. Хотя они кажутся похожими, у них есть разные значения и суть.

Цифра – это символ, который используется для обозначения числа. В общем случае, цифры составляют множество от 0 до 9. Цифры являются абстракцией, которая помогает нам понять, сколько объектов или единиц чего-либо у нас есть.

Число – это абстрактное понятие, которое представляет собой совокупность цифр или иных символов, используемых для измерения, подсчёта и математических операций.

Если цифры помещены вместе, они образуют число. Примеры чисел: 7, 92, 555. Числа могут быть целыми, рациональными, иррациональными, вещественными, комплексными и другими. В мире математики и науки числа играют важную роль и используются для описания и измерения различных физических и абстрактных величин.

Таким образом, разница между цифрой и числом заключается в том, что цифра является символом, а число представляет собой совокупность цифр и используется для измерения, подсчёта и математических операций.

Определение и характеристики чисел

В математике число — это абстрактное понятие, которое используется для измерения и подсчёта количества объектов или явлений. Числа являются основными элементами математической теории и обычно представляются в виде цифр или символов.

Главная разница между цифрой и числом заключается в их значении и использовании. Цифра — это символ, который используется для обозначения числа. Например, цифра «5» представляет собой число пять. Однако цифра сама по себе не является числом, она является только его представлением.

В математике число можно определить как элемент множества числовых значений, которое может включать в себя целые числа, дроби, рациональные и иррациональные числа. Остается суть числа содержится в его значение и свойствах.

Существует несколько характеристик чисел, которые помогают понять их свойства и отношения. Например, числа могут быть положительными, отрицательными или нулевыми. Они могут быть целыми или дробными. Кроме того, числа могут быть рациональными или иррациональными в зависимости от того, являются ли они дробями или корнями чисел.

Числа также могут быть классифицированы по размеру. Например, существуют большие и маленькие числа, а также числа, которые бесконечно малы или бесконечно большие.

В заключении, числа — это основа математики и представляют собой абстрактные объекты, которые используются для измерения и подсчёта. Они отличаются от цифр, которые являются символами, используемыми для обозначения чисел. Понимание и использование чисел является важным элементом в различных областях науки, техники и повседневной жизни.

Примеры использования чисел

Число — это абстрактная единица, которая используется для измерения или подсчета количества чего-либо. Отличие числа от цифры заключается в том, что число имеет суть, в то время как цифра является символом представления этого числа.

Примеры использования чисел:

1. Математика: в математике числа используются для выполнения арифметических операций, решения уравнений и создания математических моделей.
2. Физика: в физике числа используются для измерения физических величин, например, времени, длины, массы и скорости.
3. Финансы: в финансовой сфере числа используются для подсчета доходов, расходов, прибыли, потерь и состояния счета.
4. Естественные науки: в биологии числа используются для подсчета количества организмов, клеток и их характеристик.
5. География: в географии числа используются для измерения размеров, расстояний, площадей и координат.

Цифра, с другой стороны, используется для представления чисел в письменной или печатной форме.

Разница между числами и цифрами в том, что числа являются абстрактными и представляют собой множество, в то время как цифры являются конкретными символами, представляющими эти числа.

Примеры цифр:

• 0 — ноль
• 1 — один
• 2 — два
• 3 — три
• 4 — четыре

Использование чисел и цифр помогает нам выражать и работать с количественными и пропорциональными отношениями в различных областях знаний и деятельности.

История цифр разных народов

Цифры древней Греции

Под плеядой легендарных античных математиков и философов сформировалось две системы счисления. Каждая из них приносила свои преимущества, но они не были открыты или доработаны в связи с политико-культурными переменами.

Аттическую систему можно было бы назвать десятичной, если бы в ней не была выделена цифра 5. Аттическая запись чисел использовала повторы коллективных символов, что напоминало месопотамский метод. Единицу обозначала черта, написанная нужное количество раз. Таким образом записывались числа до 4. Цифра 5 была под первой буквой слова «пента», 10 – под первой буквой слова «дека» («десять») и т.д.

История чисел и цифр:

Алфавитная (или ионическая) система достигла своего расцвета в преддверии Александрийской эпохи. По сути, объединила десятеричную систему счисления и древневавилонский способ позиционности. Цифры записывались буквами и черточками. Система счисления довольно перспективна, но греки с их фанатичным стремлением к совершенству так и не довели ее до ума. Пытаясь достигнуть максимальной строгости и четкости в числовых записях, математики внесли существенные трудности в работу с ней.

Секреты успешных людей

Легкоузнаваемые, четкие, строгие и ясные обозначения стали весьма удачным изобретением римлян. Пройдя сквозь века, символы остались практически неизменными еще и потому, что Рим пользовался влиянием на древней государственной арене. А также перенимал некоторые культурные особенности у завоеванных народов. Бросается в глаза алфавитное обозначение цифр – главная «изюминка» аттической системы. Цифра V (5) – прототип ладони с раскрытыми пятью пальцами. Стало быть, Х (10) – две ладони. Палочками указывали единицы, а для сотен и тысяч предназначены прописные буквы алфавита.

Числа и цифры древнего Рима

Цифры древнего Китая

Система сложных, абстрактных иероглифов, в которую превратились невинные зарубки на гадальных костях, мало где применяется. Впрочем, иероглифы используются для формальных записей, а упрощенный набор символов применяется в повседневной жизни.

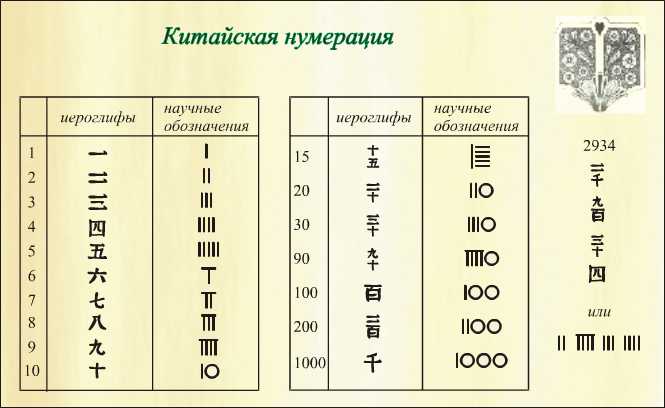
Числа в древней Руси

Как ни странно, Русь повторила алфавитную систему счисления. Каждая цифра была названа соответствующей ее рангу буквой алфавита. Цифра 1 выглядела как «А», 2 – «Б», 3 – «В» и т.д. Десятки и сотни также были подписаны соответствующими буквами славянского алфавита. Чтобы не путать в тексте слова с цифрами, над числовыми записями рисовали титло – горизонтальную волнистую линию.

числа и цифры Древней Руси

Древнеиндийские цифры

Сколько бы ни спорили ученые, сколько бы изменений ни претерпевала форма цифр, но возникновение арабских, «наших» цифр приписывают древней Индии. Возможно, арабы позаимствовали древнеиндийскую систему счисления или изобрели ее сами. Причиной научных мытарств стал фундаментальный математический труд Аль-Хорезми «Об индийском счете». Книга стала своеобразной «рекламой» десятичной позиционной системы. Иначе как объяснить внедрение индийской системы счисления на территории всего Халифата?

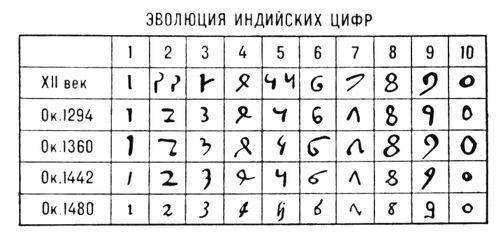
Полноценность позиционной системы укрепилась возникновением «нуля». В целом запись чисел не ушла далеко от аттической: для цифр 5, 10, 20… использовались коллективные символы, повторяющиеся нужное количество раз.

При таком подходе из древнеиндийских цифр не могли «вырасти» арабские. Это утверждение кажется логичным на первый взгляд, но история цифр загадочна, и демонстрирует непричастность древней Индии к возникновению знакомых нам символов.